![]()
1) Βρείτε και σχεδιάστε την εφαπτομένη της
f(x)=2x^3+3x^2-12x+7
στο σημείο (1, f(1))
Λύση:
![]()
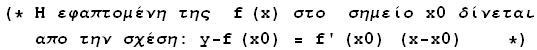
![]()
![]()
![]()
![]()
![]()
![]()
![plotf = Plot[f[x], {x, -4, 3}, DisplayFunction→Identity] ;](HTMLFiles/Askhseis_10.gif)
![ploty = Plot[efapt[x], {x, -4, 3}, DisplayFunction→Identity] ;](HTMLFiles/Askhseis_11.gif)
![]()
![[Graphics:HTMLFiles/Askhseis_13.gif]](HTMLFiles/Askhseis_13.gif)
![]()
Επειδή δεν φαίνεται ποια είναι η εφαπτόμενη, την χρωματίζουμε κόκκινη:
![plotf = Plot[f[x], {x, -4, 3}, DisplayFunction→Identity]](HTMLFiles/Askhseis_15.gif)
![ploty = Plot[efapt[x], {x, -4, 3}, PlotStyle→RGBColor[1, 0, 0], DisplayFunction→Identity]](HTMLFiles/Askhseis_16.gif)
![]()
![]()
![]()
![[Graphics:HTMLFiles/Askhseis_20.gif]](HTMLFiles/Askhseis_20.gif)
![]()
![]()
![[Graphics:HTMLFiles/Askhseis_23.gif]](HTMLFiles/Askhseis_23.gif)
![]()
2)Δίνεται η συνάρτηση f(x)που ορίζεται να είναι ίση με - ![]() για x<0 και
για x<0 και ![]() για x>=0. Να ορίσετε την συνάρτηση, να βρείτε την παράγωγό της g και να γίνει η γραφική παράσταση των f, g στο ίδιο σύστημα αξόνων.
για x>=0. Να ορίσετε την συνάρτηση, να βρείτε την παράγωγό της g και να γίνει η γραφική παράσταση των f, g στο ίδιο σύστημα αξόνων.
Λύση.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Βλέπουμε ότι η χρήση της := στον ορισμό της g δεν απέδωσε διότι η := υπολογίζει το δεξιό μέλος αφού η μεταβλητή του αριστερού μέλους (εδώ η x) πάρει μια τιμή (εδώ x=2). Δηλαδή θα υπολογίσει το D[f[2],2]!!!ενώ εμείς θέλουμε πρώτα να υπολογισθεί το δεξιό μέλος και ΜΕΤΑ η x να πάρει την τιμή 2. Αυτό ακριβώς κάνει η χρήση του (σκέτου)=. Ξαναγράφουμε τον ορισμό της g ως εξής:
![]()
Οπότε για παράδειγμα
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Παρατήρηση: Αυτό είναι φυσικά λάθος διότι ξέρουμε ότι η παράγωγος στο x0=0 είναι ακριβώς 0. Πράγματι η παράγωγος στο 0 απο δεξιά είναι ίση με
![Limit[(h^2 - 0)/h, h→0, Direction→ -1]](HTMLFiles/Askhseis_45.gif)
![]()
και απο αριστερά
![Limit[(-h^2 - 0)/h, h→0, Direction→1]](HTMLFiles/Askhseis_47.gif)
![]()
![Plot[{f[x], g[x]}, {x, -1, 1}, PlotStyle→ {GrayLevel [0], GrayLevel[.8]}]](HTMLFiles/Askhseis_49.gif)
![[Graphics:HTMLFiles/Askhseis_50.gif]](HTMLFiles/Askhseis_50.gif)
![]()
Ένας άλλος τρόπος ορισμού είναι με την χρήση της If:
![]()
![]()
![]()
3)Να λυθεί το παρακάτω σύστημα ως προς την x, y με χρήση της FindRoot, της NSolve και της γραφικής μεθόδου.
4x^2+y^2=4, x^2+4y^2=4
Λύση. Θα προσπαθήσουμε πρώτα με την NSolve
![]()
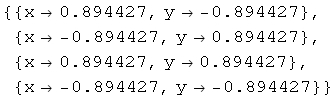
Με την FindRoot θα πρέπει να διαλέξουμε κάποιες αρχικές τιμές κοντά στις ρίζες. Για να βρούμε για παράδειγμα την πρώτη λύση θέτουμε x0=0.89 και y0=-0.89 οπότε
![]()
![]()
![FindRoot[{4x^2 + y^2 == 4, x^2 + 4y^2 == 4}, {x, x0}, {y, y0}]](HTMLFiles/Askhseis_59.gif)
![]()
H γραφική μέθοδος συνίσταται στο να γίνουν οι γραφικές παραστάσεις των δύο καμπύλων 4x^2+y^2== 4 και x^2+4y^2== 4 στο ίδιο επίπεδοκαι στην συνέχεια να ανακαλύψουμε (με το μάτι) τα κοινά σημεία (x,y) των δύο καμπυλών δηλ. ουσιαστικά τις λύσεις του συστήματος. Η μέθοδος αυτή μειονεκτεί διότι εντοπίζει μόνο τις πραγματικές λύσεις και μάλιστα όχι με μεγάλη ακρίβεια(μπορεί να χρησιμοποιηθεί για την εύρεση των x0,y0 που θα χρησιμοποιήσει αρχικά η FindRoot).
Α τρόπος. Σχεδιασμός των γραφικών παραστάσεων με την χρηση της ContourPlot:

![]()

![]()

![[Graphics:HTMLFiles/Askhseis_66.gif]](HTMLFiles/Askhseis_66.gif)
![]()
Μπαίνουμε με το ποντίκι μέσα στο σχήμα Πατώντας το πλήκτρο Ctrl και το αριστερό πλήκτρο του ποντικιού ο ρόμβος γίνεται σταυρός που οι συντεταγμένες του κέντρου του εμφανίζονται στο παράθυρο κάτω αριστερά. Όπως βλέπουμε υπάρχουν 4 λύσεις (1 σε κάθε τεταρτημόριο).
Β τρόπος. Σχεδιασμός των γραφικών παραστάσεων με την χρηση της ImplicitPlot:
![]()
![cp11 = ImplicitPlot[4x^2 + y^2 == 4, {x, -3, 3}, PlotPoints→120, DisplayFunction→Identity]](HTMLFiles/Askhseis_69.gif)
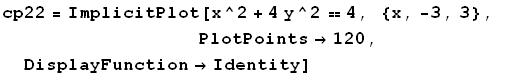
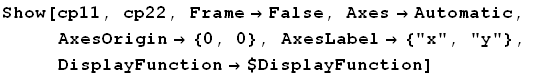
![[Graphics:HTMLFiles/Askhseis_72.gif]](HTMLFiles/Askhseis_72.gif)
![]()
4)Δίνεται η ακολουθία f[x_, k_]:=x^(3k). Να βρεθεί το άθροισμα ![]() f[x,k] για τις διάφορες τιμές του x και ανακαλύψτε για ποια x το άθροισμα δεν υπάρχει.
f[x,k] για τις διάφορες τιμές του x και ανακαλύψτε για ποια x το άθροισμα δεν υπάρχει.
![]()
![]()
![]()
Φυσικά αυτό δεν είναι σωστό για παράδειγμα για x=2 το αποτέλεσμα δεν ειναι -![]() /.x->2 αλλά
/.x->2 αλλά
![Underoverscript[∑, k = 1, arg3] f[2, k]](HTMLFiles/Askhseis_79.gif)
![]()
![]()
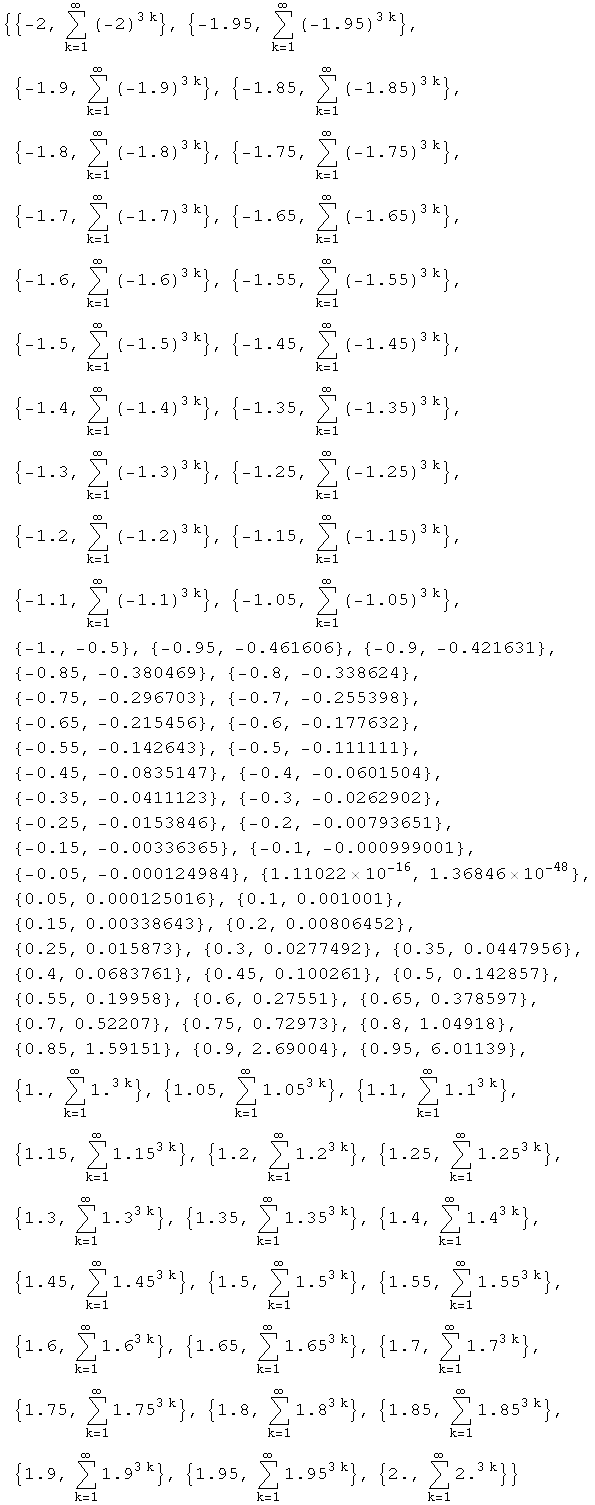
δηλ. αποκλίνει!!! Για να δούμε την συμπεριφορά των αθροισμάτων, θα βρούμε τα αθροισματα για κάμποσες τιμές του x και θα τα βάλουμε σε ένα πίνακα.Π.χ στο διάστημα [-2,2] έχουμε την παρακάτω συμπεριφορά
![]()
![]()
![]()
![]()
![]()

Απ΄οτι φαίνεται για τιμές μεγαλύτερες του 1 ή μικρότερες του -1 το άθροισμα αποκλίνει. Ας προσπαθήσουμε να σχεδιάσουμε την γραφική παράσταση με την χρήση της Interpolation χρησιμοποιώντας το παραπάνω δείγμα τιμών: Ας παρουμε καταρχήν σε ένα πίνακα τα ζεύγη τιμών {x, ![]() f[x,k] }
f[x,k] }
![pinakas = Table [{x, Sum[f[x, k], {k, 1, Infinity}]}, {x, -2, 2, 0.05}]](HTMLFiles/Askhseis_89.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
και ας ζωγραφίσουμε τώρα την InterpolatingFunction δηλ. την συνάρτηση που προκύπτει απο τα σημεία του pinakas με την μέθοδο της παρεμβολής:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Askhseis_114.gif]](HTMLFiles/Askhseis_114.gif)
![]()
Από το σχήμα πάλι φαίνεται ότι η δοθείσα σειρά συγκλίνει μόνο για x στο διάστημα -1...1 χωρίς τα άκρα.
Ας ζωγραφίσουμε τώρα και την -![]() περίπου στο ίδιο διάστημα
περίπου στο ίδιο διάστημα
![Plot[-x^3/(-1 + x^3), {x, -2, 2}, PlotRange→ {-0.7, 0.7}]](HTMLFiles/Askhseis_117.gif)
![[Graphics:HTMLFiles/Askhseis_118.gif]](HTMLFiles/Askhseis_118.gif)
![]()
Συγρίνοντας τις δυο παραπάνω γραφικές παραστάσεις υποπτευόμαστε ότι ο τύπος του ορίου -![]() που έδωσε ως απάντηση το Mathematica, είναι σωστός μόνο για x στο ανοικτό διάστημα (-1,1) και για οποιαδήποτε άλλη τιμή του x δεν είναι σωστός.
που έδωσε ως απάντηση το Mathematica, είναι σωστός μόνο για x στο ανοικτό διάστημα (-1,1) και για οποιαδήποτε άλλη τιμή του x δεν είναι σωστός.
Ένας άλλος πιό εύκολος τρόπος να δούμε το παραπάνω συμπέρασμα με μαθηματική αυστηρότητα, είναι να θεωρήσουμε τα μερικά αθροίσματα:
![]()
![]()
και να κάνουμε τις απλοποίησεις
![]()
![]()
και να πάρουμε το όριο για n->Infinity. Αυτό συγκλίνει μόνο για x στο ανοικτό διάστημα (-1,1). Το προκύπτον όριο είναι -![]() . Αυτό βγαίνει διότι ως γνωστό από τα μαθηματικά το Limit[x^( 3n), n->Infinity] συγκλίνει (στο 0)μόνο για x μεταξύ -1,...,1. ( Όμως αν ζητήσομε απο το Mathematica να μας βρεί τό όριο της
. Αυτό βγαίνει διότι ως γνωστό από τα μαθηματικά το Limit[x^( 3n), n->Infinity] συγκλίνει (στο 0)μόνο για x μεταξύ -1,...,1. ( Όμως αν ζητήσομε απο το Mathematica να μας βρεί τό όριο της ![]() ή της x^n για n ->Infinity δυστυχώς θα απογοητευτούμε διότι δεν θα ξέρει πόσο είναι!!!)
ή της x^n για n ->Infinity δυστυχώς θα απογοητευτούμε διότι δεν θα ξέρει πόσο είναι!!!)
5)Να υπολογιστεί η 8ης τάξη προσέγγιση της
f(x) = e^( -(x - 1)^2 (x + 1)^2 )
γύρω απο το σημείο x=1. Να σχεδιαστεί η f(x) και η προσέγγιση.

![[Graphics:HTMLFiles/Askhseis_128.gif]](HTMLFiles/Askhseis_128.gif)
![]()
6)Να βρεθεί τό όριο ![]()
![]()
Λύση. Έχουμε
![]()

Ωχ! Τι είναι αυτό; Ας το αλλάξουμε λίγο
![]()
![]()
δηλ. μοιάζει να προσθέτουμε τους πραγματικούς Sin[x]/x και να παίρνουμε όριο ένα Μιγαδικό!!! Παράλογο! Ας κάνουμε μια μικρή απλοποίηση
![]()
![]()
Ας κάνουμε περισσότερη απλοποίηση...
![]()
![]()
Ουφ...και τρομάξαμε...Άλλος τρόπος χωρίς FullSimplify
![]()
![]()
δηλ. είναι ουσιαστικά πραγματικός. Το 1.0707963268 δεν είναι άλλο παρά η προσέγγιση του ![]() (-1+π)
(-1+π)
![]()
![]()
![]()
7)Τρείς ακέραιοι επιλέγονται τυχαία απο τους 1,2...,1000. Με πόσους τρόπους είναι δυνατον να επιλεγούν οι ακέραιοι αυτοί, ώστε το άθροισμά τους να διαιρείται με το 4; (Άσκηση 3.29 σελ. 121 απο το βιβλίο Στοιχεία διακριτών Μαθηματικών του C.L.Liu που μοιράζεται στους φοιτητές μας)
Καταρχήν θα μπορούσε καποιος να γράψει ένα πρόγραμμα που θα καταμετρά τις διαφορετικές τριάδες {r,n,m} με 1<=r<=n<=m<=1000 με την ιδιότητα το 4 να διαιρεί το r+m+n. Ένα τέτοιο πρόγραμμα είναι το παρακάτω....
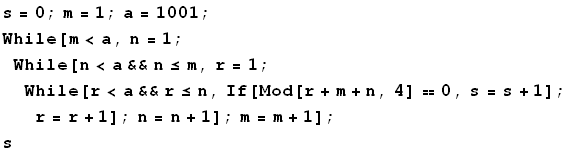
Θα έλεγα όμως να μην το τρέξετε θα καθυστερήσει πάρα πολύ!! Υπάρχει όμως και άλλη μια ιδέα: Να σκεφτούμε και λίγο ως μαθηματικοί....Τα δυνατά υπόλοιπα ενός αριθμού 1<=r<=1000με το 4 είναι 0,1,2ή 3. Οπότε για να διαιρεί το 4 το r+m+n θα πρέπει το άθροισμα των υπολοίπων Mod[r,4]+Mod[m,4]+Mod[n,4] να είναι πολλαπλάσιο του 4 , οπότε θα πρέπει να έχουμε μια απο τις παρακάτω περιπτώσεις
1)Mod[r,4]=Mod[m,4]=Mod[n,4]=0(άθροισμα 0)
2)κάποιο απ'τα {r,n,m} να δίνει υπόλοιπο 0 και τα υπόλοιπα δυο, υπόλοιπο 2(άθροισμα 4)
3)κάποιο απ'τα {r,n,m} να δίνει υπόλοιπο 2και τα υπόλοιπα δυο, υπόλοιπο 1(άθροισμα 4)
4)κάποιο απ'τα {r,n,m} να δίνει υπόλοιπο 2και τα υπόλοιπα δυο, υπόλοιπο 3(άθροισμα 8)
5)κάποιο απ'τα {r,n,m} να δίνει υπόλοιπο 0, το άλλο 1 και το άλλο 3.(άθροισμα 4)
Κάτι επίσης γνωστό απο την θεωρία, οι αριθμοί μεταξύ 1...α που διαιρούνται με κάποιο β<α είναι πλήθους Ceiling[α/β]. (μάθετε απο το Help ποιά είναι η Ceiling). Με όμοιο τρόπο αποδεικνύεται ότι υπάρχουν Ceiling[α/β] αριθμοί <=α που δίνουν ακριβώς υπόλοιπο ρ( όπου ρ μεταξύ 0...β-1 )όταν διαιρεθούν με β. Έτσι για α=1000και β=4 και ρ=2 έχουμε
![]()
![]()
αριθμούς <=1000 και μεγαλύτερους του 0, που δίνουν ακριβώς υπόλοιπο 2. Τώρα αν διαλέξουμε δυο αριθμούς απο αυτούς έστω κ1,κ2 με κ1<=κ2 τότε υπάρχουν 250*251/2 τέτοια ζευγάρια (γιατί;). Οπότε το πλήθος των τριάδων για την περίπτωση (2) είναι 250(αριθμοί που δίνουν υπόλοιπο 0)* 250*251/2 (ζευγάρια αριθμών που δίνουν υπόλοιπο 2) =250*250*251/2=
![]()
![]()
Όμοια δουλεύομε στις περιπτώσεις 3)και 4). Για την 5) περίπτωση όλοι οι αριθμοί ανήκουν σε διαφορετικά γκρούπ αριθμών οπότε έχουμε
![]()
![]()
διαφορετικές τριάδες. Τέλος για την περίπτωση (1) θέλουμε απο το γκρουπ G των αριθμών 1...1000 που δίνουν υπόλοιπο 0 με το 4(δηλ. τα πολλαπλάσια του 4) να καταμετρήσουμε τις τριάδες {r,n,m} με r<=n<=m. Έστω οτι οι αριθμοί στο G είναι οι α[1],α[2],...,α[250] και έχουν μπεί σε αύξουσα σειρά
![]()
οπότε με το παρακάτω πρόγραμμα καταμετρούμε τις τριάδες {α[i],α[j],α[k]} του G, με i<=j<=k (την απάντηση την δίνει παρακάτω το s)
![s = 0 ; k = 1 ; While[k≤250, j = 1 ; While[j≤250&& (j≤k), i = 1 ; While[i≤250&& (i≤j), s = s + 1 ; i = i + 1] ; j = j + 1] ; k = k + 1] ; s](HTMLFiles/Askhseis_154.gif)
![]()
η πιό απλά με χρήση της Do
![s = 0 ; Do[s = s + 1, {k, 1, 250}, {j, 1, k}, {i, 1, j}] ; s](HTMLFiles/Askhseis_156.gif)
![]()
Άρα η τελική απάντηση είναι
![]()
![]()
8)Στο πείραμα ρίψης ενός ζαριού να βρεθεί η πιθανότητα να πάρουμε ένα περιττό αριθμό.
Α' τρόπος(ορισμός της πιθανότητος ως το πηλίκο ευνοικές περιπτώσεις προς όλες τις περιπτώσεις). Προφανώς όλες οι δυνατές περιπτώσεις είναι 6 και οι ευνοικές μόνο 3 άρα 6/3= 1/2 η ζητούμενη πιθανότητα. Για χάρην όμως παραδείγματος θα βρούμε τις ευνοικές με χρήση του Mathematica... Κατ'αρχην να φτιάξουμε ένα test που να μας δίνει True όταν ειμαστε σε ευνοική περίπτωση:
![]()
![]()
![]()
![]()
![]()
οπότε οι ευνοικές περιπτώσεις με χρήση της Select είναι:
![]()
![]()
με πλήθος ίσο με
![]()
![]()
οπότε η ζητούμενη πιθανότητα είναι
![]()
![]()
Β' τρόπος( ορισμός της πιθανότητος με χρήση στατιστικών δεδομένων). Θα χρησιμοποιήσουμε το Mathematica για να μας κάνει τις καταμετρήσεις των ευνοικών περιπτώσεων για οσοδήποτε μεγάλο αριθμό ρίψεων. Θα χρησιμοποιήσουμε την Random[Integer,{1,6}] για να ρίχνουμε το ζάρι( όσες φορές θέλουμε π.χ n φορές). Για την καταμέτρηση των ευνοικών περιπτώσεων φτιάχνουμε την συνάρτηση f
![f[n_] := If[n == 0, 0, Module[{s = 0}, Do[If[Mod[Random[Integer, {1, 6}], 2] == 0, s = s, s = s + 1], {n}] ; s]]](HTMLFiles/Askhseis_171.gif)
Κάθε φορά που εκτελείται η f δίνει και διαφορετικό αποτέλεσμα, π.χ για n=10 ρίψεις
![]()
![]()
![]()
![]()
![]()
![]()
δηλαδή η f δεν είναι συνάρτηση με την μαθηματική έννοια διότι για το ίδιο αριθμό ρίψεων κάθε φορά που εκτελούμε το πείραμα(την f) θα πάρουμε και διαφορετικό αποτέλεσμα!!
Η (μερική)πιθανότητα είναι ίση μεf[n]/n. Θα θεωρήσουμε τώρα το όριο της μερικής πιθανότητος f[n]/n για n->∞. Αυτή θα είναι η ζητούμενη πιθανότητα.
![]()
![]()
![]()
![]()
Ωχ η Limit δεν δούλεψε...Αυτό είναι φυσικό διότι η Limit χρησιμοποιεί αναλυτικές και συμβολικές μεθόδους και άρα για να βρούμε το Limit θα έπρεπε να είχαμε μια "απλή" συνάρτηση (ή που να ορίζεται μέσω απλών συναρτήσεων). Άλλη ιδέα: Να βρούμε το κλάσμα s=f[n]/n για ένα πολύ μεγάλο n ρίψεων π.χ για n=100000 ρίψεις. Για να σιγουρευτούμε ότι είμαστε κόντα στο ακριβές όριο(αυτό που ψάχνουμε...)ξανακάνουμε το πείραμα για δεύτερη φορά και βρίσκουμε το s1=f[n]/n . Αν η διαφορά τους είναι πολύ μικρή (< κάποιου ε) σταματάμε και δίνουμε απάντηση (όριο)το s, αλλιώς επαναλαμβάνουμε το πείραμα αλλά για n μεγαλύτερο. Εκεί που θα σταματήσει το παραπάνω πρόγραμμα, θα έχουμε βρεί το όριο(την πιθανότητα) με την ζητούμενη ακρίβεια...Επειδή δεν ξέρουμε το ακριβές πλήθος βημάτων θα χρησιμοποιήσουμε την While.
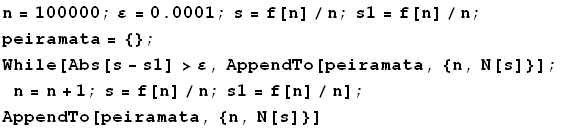

Στα peiramata βάζουμε όλα τα αποτελέσματα των πειραμάτων που εκτελέσαμε... Παρακάτω δίνονται άλλες δυο προσεγγίσεις για το πρόβλημα της εύρεσης του ορίου. Η πρώτη μέθοδος χρησιμοποιεί την NLimit που βρίσκεται μέσα στο πακέτο NumericalMath`NLimit` και η δεύτερη μέθοδος χρησιμοποιεί την SequenceLimit για να βρίσκει το "όριο" μιας ακολουθίας τιμών που βρίσκεται μέσα σε ένα (πεπερασμένο)πίνακα. Για περισσότερες πληροφορίες για τις συναρτήσεις αυτές πηγαίνετε στο Help.
![]()
![(*1*)Clear[r] ; NLimit[f[r]/r, r→Infinity, Method→SequenceLimit]](HTMLFiles/Askhseis_185.gif)
![]()
![(*2*)pinakas = Table[f[n]/n, {n, 200000, 800000, 200000}] ;](HTMLFiles/Askhseis_187.gif)
![]()
![]()
9)Να ορίσετε την μέση τιμή μιας λίστας x από αριθμούς.
Λύση. Το Length[x] δίνει το πλήθος των στοιχείων της λίστας x, και η μέση τιμή ορίζεται σαν το άθροισμα των στοιχείων x[[i]] της x προς το πλήθος των στοιχείων της...
![]()
![]()
![]()
![]()
![]()
10)Να βρεθεί το εμβαδό του χωρίου μεταξύ των καμπυλών Sin[x] και Cos[x] για x στο διάστημα [0,2Pi].
Λύση.
![]()
![[Graphics:HTMLFiles/Askhseis_196.gif]](HTMLFiles/Askhseis_196.gif)
![]()
Για να βρούμε το εμβαδόν του χωρίου παίρνουμε την απόλυτη διαφορά τους
![]()
και χρησιμοποιούμε την NIntegrate( η Intergrate δεν χρησιμοποιείται διότι η f[x] ορίζεται με μια όχι και τόσο απλή συνάρτηση όπως η Abs και δεν γνωρίζουμε να ολοκληρώσουμε τέτοιες συναρτήσεις με τις αναλυτικές μεθόδους που χρησιμοποιούνται στην Integrate). Έχουμε και εδώ το πρόβλημα που είχαμε και με τον ορισμό του ορίου μιας όχι καλής συνάρτησης στην άσκηση 8.
![Plot[{ Sin[x], Cos[x], f[x] }, {x, 0, 2Pi}, PlotStyle→ {{}, {}, RGBColor[1, 0, 0]}] ;](HTMLFiles/Askhseis_199.gif)
![[Graphics:HTMLFiles/Askhseis_200.gif]](HTMLFiles/Askhseis_200.gif)
Μας ενδιαφέρει το εμβαδόν που βρίσκεται μεταξύ των δυο καμπύλων το οποίο είναι φυσικά ίσο με το εμβαδόν που βρίσκεται μεταξύ του άξονα Ox και της κόκκινης γραμμής...
![]()
![]()
11)Να βρεθεί το άνω φράγμα για το σφάλμα 4ης τάξης της προσέγγισης Mclaurin της συνάρτησης f(x)=x/(x^2+1), στο διάστημα [0, 1/2]. Είναι γνωστό απο την θεωρία ότι το υπόλοιπο(ή σφάλμα) είναι της μορφής ![]()
![]() όπου
όπου ![]() (y)είναι η πέμπτη παραγωγος της f σε κάποιο σημείο y διαστήματος.
(y)είναι η πέμπτη παραγωγος της f σε κάποιο σημείο y διαστήματος.
Λύση.
![]()
Κατ' αρχήν η σειρά McLaurin (γύρω απο το σημείο 0) της f[x] 4ης τάξεως, είναι
![]()
![]()
Το σφάλμα ![]() όπως μας λέει η εκφώνηση είναι της μορφής
όπως μας λέει η εκφώνηση είναι της μορφής ![]()
![]() και ψάχνουμε την χειρότερη μέγιστη τιμή που μπορεί να πάρει. Ας δούμε λίγο την γραφική παράσταση της
και ψάχνουμε την χειρότερη μέγιστη τιμή που μπορεί να πάρει. Ας δούμε λίγο την γραφική παράσταση της ![]() (y)/5!για διάφορες τιμές της y
(y)/5!για διάφορες τιμές της y
![]()
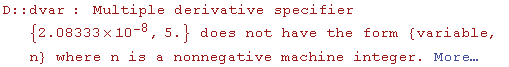
![]()
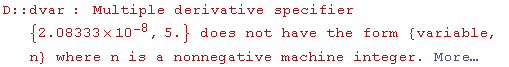
![]()
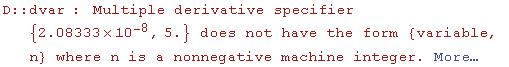
![]()
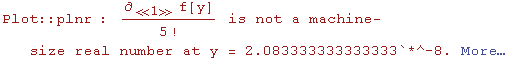
![]()
![]()

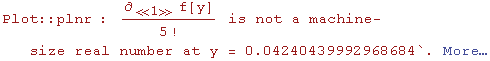
![]()
![[Graphics:HTMLFiles/Askhseis_226.gif]](HTMLFiles/Askhseis_226.gif)
![]()
Ωχ! Ξεχάσαμε την Evaluate( H Plot σχεδιάζει μόνο συναρτήσεις!!Παίρνει κάποια δειγματικά σημεία x απο το πεδίο ορισμού και τα βάζει στην συνάρτηση, βρίσκει το y....και τα προκύπτοντα σημεία (x,y) τα ενώνει και προκύπτει η γραφ. παράσταση. Όταν βάζει η Plot μια τιμή y στην παράγωγο D[f[y],{y,5}] τότε δημιουργείτε το πρόβλημα διότι δεν πρέπει να αντικαταστήσουμε την y στην παράγωγο πριν υπολογίσουμε την ίδια την παράγωγο ! Αυτήν την δουλειά κάνει η Evaluate. Αλλάζει την σειρά εκτέλεσης των εντολών. Έτσι πρώτα υπολογίζεται η παράγωγος(ως μία συνάρτηση του y) και μετά η Plot αρχίζει το έργο της...
![]()
![[Graphics:HTMLFiles/Askhseis_229.gif]](HTMLFiles/Askhseis_229.gif)
![]()
Απ' οτι βλέπουμε η μέγιστη τιμή είναι περίπου 1. Άλλος τρόπος είναι με την εύρεση του μεγίστου με την χρήσης της - FindMinimum
![]()
![]()
δηλ. ακριβώς 1 στο σημείο 0!! Άρα το άνω φράγμα του σφάλματος είναι x^5.
Τέλος ας σχεδιάσουμε την f[x] , την σειρά χωρις το σφάλμα και την σειρά με το (μέγιστο) σφάλμα γύρω απο το 0:
![]()
![Plot[{f[x], seiraxwrisfalma[x], seiraxwrisfalma[x] + x^5 }, {x, 0, 1/2}, PlotStyle→ {Dashing[{0.01}], GrayLevel[0], RGBColor[1, 0, 0]}]](HTMLFiles/Askhseis_234.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Askhseis_243.gif]](HTMLFiles/Askhseis_243.gif)
![]()
Ωχ πάλι ξεχάσαμ ε το Evaluate για να βρούμε πρώτα την seiraxwrisfalma και μετά την Plot (η seiraxwrisfalma μάλλον την μπέρδεψε την Plot!...έχουμε το ίδιο προβλημα όπως και παραπάνω)
![Plot[Evaluate[{f[x], seiraxwrisfalma[x], seiraxwrisfalma[x] + x^5}], {x, 0, 1/2}, PlotStyle→ {Dashing[{0.01}], GrayLevel[0], RGBColor[1, 0, 0]}]](HTMLFiles/Askhseis_245.gif)
![[Graphics:HTMLFiles/Askhseis_246.gif]](HTMLFiles/Askhseis_246.gif)
![]()
To GrayLevel[0] είναι το απόλυτο μαύρο (για την seiraxwrisfalma[x]), το Dashing[{0.01}] είναι για να βγεί η f[x] με διακεκομμένες...παρατηρείστε ότι καθώς το x απομακρύνεται απο το 0 τόσο εμφανίζεται το σφάλμα ...στην προσέγγιση της f με MacLaurin.
12) Δίνεται η συνάρτηση
![]()
Να γίνει η γραφική της παράσταση, για x στο [1,5] και στην συνέχεια χρησιμοποιώντας την ParametricPlot3D να σχεδιάσετε τριδιάστατα την επιφάνεια που προκύπτει απο την περιστροφή της f γύρω απο 1)τον άξονα Ox και 2) γύρω απο τον άξονα Οy(των τιμών)
Λύση.
![]()
![[Graphics:HTMLFiles/Askhseis_250.gif]](HTMLFiles/Askhseis_250.gif)
![]()
Η εξίσωση της επιφάνειας εκ περιστροφής γύρω απο τον άξονα Ox, με χρήση κυλινδρικών συντεταγμένων:
![]()
![]()
![]()

![[Graphics:HTMLFiles/Askhseis_256.gif]](HTMLFiles/Askhseis_256.gif)
![]()
Η εξίσωση της επιφάνειας εκ περιστροφής γύρω απο τον άξονα Oy, με χρήση κυλινδρικών συντεταγμένων:
![]()
![]()
![]()
![ParametricPlot3D[{x[r, t], y[r, t], z[r, t]}, {r, 1, 5}, {t, -Pi, Pi}, PlotPoints→30, AxesLabel→ {"Ox", "Oy", "Oz"}] ;](HTMLFiles/Askhseis_261.gif)
![[Graphics:HTMLFiles/Askhseis_262.gif]](HTMLFiles/Askhseis_262.gif)
13)Δίνεται η
![]()
Να σχεδιαστεί η τομή της παραπάνω επιφάνειας με τα επίπεδα: 1)x=5 2)y=6 και 3)x=y
Λύση.
![]()
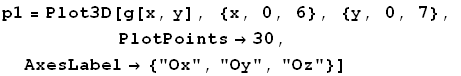
![[Graphics:HTMLFiles/Askhseis_266.gif]](HTMLFiles/Askhseis_266.gif)
![]()
1)Η τομή της επιφάνειας με το επίπεδο είναι μια καμπύλη που έχει παραμετρικές εξισώσεις
![]()
οπότε η γραφική παράστασή της είναι
![p2 = ParametricPlot3D[{x, y, z}, {t, -1, 7}, PlotRange→ {{0, 6}, {-1, 7}, {-1, 1}}] ;](HTMLFiles/Askhseis_269.gif)
![[Graphics:HTMLFiles/Askhseis_270.gif]](HTMLFiles/Askhseis_270.gif)
και οι δύο μαζί
![]()
![[Graphics:HTMLFiles/Askhseis_272.gif]](HTMLFiles/Askhseis_272.gif)
![]()
Όμοια δουλεύομε για την περίπτωση 2) ενώ για την περίπτωση 3) η παραμετρικοποίηση είναι
![]()
και η γραφική παράσταση
![p3 = ParametricPlot3D[{x, y, z}, {t, -1, 7}, PlotRange→ {{0, 6}, {-1, 7}, {-1, 1}}] ;](HTMLFiles/Askhseis_275.gif)
![[Graphics:HTMLFiles/Askhseis_276.gif]](HTMLFiles/Askhseis_276.gif)
![]()
14)Να αποδειχθεί ότι μεταξύ 6 τυχαίων ατόμων ενός χωριού η πιθανότητα όταν επιλέξουμε τυχαία τρείς απ' αυτούς να είναι όλοι μεταξύ τους γνωστοί είναι ακριβώς 1/8 . (υποθέτουμε ότι η πιθανότητα να είναι κάποιος γνωστός με κάποιο άλλο συγχωριανό του είναι ακριβώς 1/2)
Ο δειγματικός χώρος μας αποτελείται απο 6 -δες τις μορφης (x1,x2,x3,x4,x5,x6) όπου (x1,x2,x3) κάποια τριάδα απ'αυτούς και x4=0 ανν είναι οι x1,x2 γνωστοί και x4=1 σε οποιαδήποτε άλλη περίπτωση. Ομοια x5=0 ανν οι x1,x3 γνωστοί και x5=1 σε οποιαδήποτε άλλη περίπτωση, και x6=0 ανν οι x2,x3 γνωστοί και x6=1 σε οποιαδήποτε άλλη περίπτωση Παρακάτω βάζουμε μέσα στο pinakas όλες τις δυνατές περιπτώσεις!
![pinakas = Flatten[Table[{x1, x2, x3, x4, x5, x6}, {x1, 1, 6}, {x2, x1 + 1, 6}, {x3, x2 + 1, 6}, {x4, 0, 1}, {x5, 0, 1}, {x6, 0, 1}], 5]](HTMLFiles/Askhseis_278.gif)

![]()
![]()
Οι ευνοικές περιπτώσεις είναι εκείνες που έχουμε
![Length[Select[pinakas, (#1[[4]] == 0&[[5]] == 0&[[6]] == 0) &]]](HTMLFiles/Askhseis_282.gif)
![]()
Άρα η πιθανότητα είναι 20/160
![]()
![]()
15)Βρείτε το εφαπτόμενο επίπεδο στην επιφάνεια f[x,y]=4/(x^2+y^2+1)στο σημείο (1/2, 1). Να γίνει και η γραφική παράσταση.
έχουμε
![]()
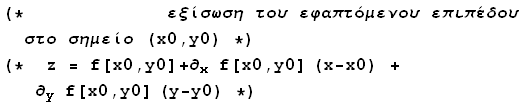
![plotf = Plot3D[f[x, y], {x, -2, 2}, {y, -2, 2}, PlotPoints→50, PlotRange→ {0, 4}, BoxRatios→ {1, 1, 1}, DisplayFunction→Identity] ;](HTMLFiles/Askhseis_288.gif)
Εύρεση μερικών παραγώγων..
![]()
![]()
![]()
![]()
Εξίσωση εφαπτόμενου επιπέδου..
![]()
![]()
![plotz = Plot3D[z, {x, -2, 2}, {y, -2, 2}, DisplayFunction→Identity] ;](HTMLFiles/Askhseis_295.gif)
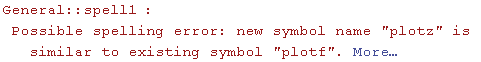
![Show[plotf, plotz, DisplayFunction→$DisplayFunction, ViewPoint-> {-3.647, 2.607, 0.488}]](HTMLFiles/Askhseis_297.gif)
![[Graphics:HTMLFiles/Askhseis_298.gif]](HTMLFiles/Askhseis_298.gif)
![]()
| Created by Mathematica (December 11, 2005) |