ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩMΑ
Ο Διανυσματικός
Λογισμός (Aναλυτική Γεωμετρία) είναι μια μαθηματική θεωρία, η. εξέλιξη της οποίας έχει
δεχτεί σημαντικές επιδράσεις από τη Φυσική.,
 Ο
γνωστός «κανόνας του παραλληλογράμμου», σύμφωνα με τον οποίο το μέγεθος και η
διεύθυνση της συνισταμένης 2 δυνάμεων που επενεργούν στο ίδιο σημείο,
εκφράζονται από τη διαγώνιο του παραλληλογράμμου που σχηματίζουν, ήταν γνωστός
από την αρχαιότητα και εμφανίζεται σε διάφορες μορφές σε έργα του Αριστστέλη,
του Αρχιμήδη και του Ήρωνα. Αυτός ο κανόνας, που υποβάλλει την ιδέα μιας
γεωμετρικής πρόσθεσης, διαφορετικής από
την κοινή πρόσθεση των ευθύγραμμων τμημάτων της Ευκλείδειας γεωμετρίας
χρησιμοποιήθηκε πολλούς αιώνες για το γεωμετρικό προσδιορισμό της συνισταμένης χωρίς ωστόσο να συμβάλει άμεσα στην
αναγνώριση μιας τέτοιας πρόσθεσης.
Ο
γνωστός «κανόνας του παραλληλογράμμου», σύμφωνα με τον οποίο το μέγεθος και η
διεύθυνση της συνισταμένης 2 δυνάμεων που επενεργούν στο ίδιο σημείο,
εκφράζονται από τη διαγώνιο του παραλληλογράμμου που σχηματίζουν, ήταν γνωστός
από την αρχαιότητα και εμφανίζεται σε διάφορες μορφές σε έργα του Αριστστέλη,
του Αρχιμήδη και του Ήρωνα. Αυτός ο κανόνας, που υποβάλλει την ιδέα μιας
γεωμετρικής πρόσθεσης, διαφορετικής από
την κοινή πρόσθεση των ευθύγραμμων τμημάτων της Ευκλείδειας γεωμετρίας
χρησιμοποιήθηκε πολλούς αιώνες για το γεωμετρικό προσδιορισμό της συνισταμένης χωρίς ωστόσο να συμβάλει άμεσα στην
αναγνώριση μιας τέτοιας πρόσθεσης.
Στη διάρκεια του
17ου αιώνα, η ιδιαίτερη έμφαση που δόθηκε στη μελέτη φυσικών ποσοτήτων όπως η
ταχύτητα, η δύναμη, η ορμή και η επιτάχυνση, οι οποίες χαρακτηρίζονται τόσο από
το μέγεθος όσο και από τη διεύθυνση τους, καθώς και η συστηματική χρήση των
αρνητικών αριθμών, έφεραν στο προσκήνιο τις έννοιες του προσανατολισμένου
ευθύγραμμου τμήματος και της
προσανατολισμένης κίνησης. Ο Newton για παράδειγμα στα μαθήματα Άλγεβρας που
έγραψε την περίοδο 1673-1683, αναφέρει τα εξής:
Μια προέλαση
μπορεί να ονομαστεί θετική κίνηση και μια υποχώρηση αρνητική κίνηση, επειδή η
πρώτη αυξάνει την πορεία που έχει ήδη γίνει, ενώ η δεύτερη την ελαττώνει. Με
τον ίδιο τρόπο στη γεωμετρία αν ένα
τμήμα σχεδιασμένο προς μια κατεύθυνση Θεωρηθεί ως θετικό; τότε το αρνητικό του
είναι ένα τμήμα cχεδιασμένο προς την
αντίθετη κατεύθυνση. Π.χ, αν το ΑΒ έχει κατεύθυνση προς τα δεξιά και το
 BC
προς αριστερά και το ΑΒ ορίζεται να είναι Θετικό, τότε το BC θεωρείται ως
αρνητικό- επειδή, όπως είναι σχεδιασμένο, ελαττώνει το ΑΒ περιορίζοντάς το στο
βραχύτερο μήκος AC ή στο τίποτα, αν το C συμπίπτει με το Α ή στο λιγότερο από
το τίποτα αν το BC είναι μεγαλύτερο από το τμήμα ΑΒ, από το οποίο αφαιρείται.
BC
προς αριστερά και το ΑΒ ορίζεται να είναι Θετικό, τότε το BC θεωρείται ως
αρνητικό- επειδή, όπως είναι σχεδιασμένο, ελαττώνει το ΑΒ περιορίζοντάς το στο
βραχύτερο μήκος AC ή στο τίποτα, αν το C συμπίπτει με το Α ή στο λιγότερο από
το τίποτα αν το BC είναι μεγαλύτερο από το τμήμα ΑΒ, από το οποίο αφαιρείται.
Είναι
αξιοσημείωτο ότι την ίδια περίοδο G.W. Leίbnίz σε επιστολή του προς τον Χ.
Huygens (8 Σεπτεμβρίου 1679), διατυπώνει ορισμένες γενικές ιδέες για την
ανάπτυξη ενός γεωμετρικού λογισμού, ο οποίος θα επιτρέπει να εκφράζονται
απευθείας, «ακόμη και χωρίς σχήματα», η θέση, οι γωνίες και η κίνηση σε
αντίθεση προς τον αλγεβρικό λογισμό που εκφράζει μόνο το μέγεθος των ποσοτήτων.
Οι ιδέες αυτές, δηλαδή η ανάπτυξη ενός
νέου λογισμού με προσανατολισμένα μεγέθη, άρχισαν να αναπτύσσονται στα
Μαθηματικά προς τα τέλη του 18ου αιώνα, σε στενή σχέση με το ζήτημα της
γεωμετρικής ερμηνείας των μιγαδικών αριθμών. Η πρώτη σημαντική εργασία πάνω σ
αυτό το ζήτημα οφείλεται στον χαρτογράφο G. Wessel και δημοσιεύτηκε το1799, με
τον χαρακτηριστικό τίτλο «Πραγματεία για την αναλυτική παράσταση της
διεύθυνσης». Σ αυτήν την εργασία γίνεται μια απόπειρα επέκτασης, από την απλή
περίπτωση των ευθύγραμμων τμημάτων που έχουν την ίδια ή αντίθετες διευθύνσεις
(και εκφράζονται αναλυτικά με τη βοήθεια των θετικών ή αρνητικών αριθμών) στη
γενικότερη περίπτωση τμημάτων του επιπέδου με τυχαίες διευθύνσεις.
Ο Wessel
ορίζει αρχικά την πρόσθεση των (προσανατολισμένων) τμημάτων και στη
συνέχεια περιγράφει τη διαδικασία πολλαπλασιασμού δυο τμημάτων.
Δυο ευθύγραμμα τμήματα μπορούν να προστεθούν, αν τα ενώσουμε με τέτοιο τρόπο, ώστε το δεύτερο να αρχίζει εκεί που τελειώνει το πρώτο και φέρουμε κατόπιν ένα ευθύγραμμο τμήμα από το αρχικό ως το τελικό σημείο των ενωμένων τμημάτων. Αυτό το τμήμα είναι το άθροισμά τους
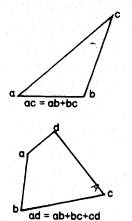 Αν θέλουμε να ενώσουμε περισσότερα από δυο
ευθύγραμμα τμήματα ακολουθούμε την ίδια διαδικασία. Τα ενώνουμε συνδέοντας το
τελικό σημείο του πρώτου με το αρχικό σημείο του δεύτερου, το τελικό σημείο του
δεύτερου με το αρχικό του τρίτου κ.ο.κ. Κατόπιν φέρνουμε ένα ευθύγραμμο τμήμα
από το σημείο που αρχίζει το πρώτο μέχρι το σημείο που καταλήγει το τελευταίο
αυτό το τμήμα το ονομάζουμε άθροισμά τους:
Αν θέλουμε να ενώσουμε περισσότερα από δυο
ευθύγραμμα τμήματα ακολουθούμε την ίδια διαδικασία. Τα ενώνουμε συνδέοντας το
τελικό σημείο του πρώτου με το αρχικό σημείο του δεύτερου, το τελικό σημείο του
δεύτερου με το αρχικό του τρίτου κ.ο.κ. Κατόπιν φέρνουμε ένα ευθύγραμμο τμήμα
από το σημείο που αρχίζει το πρώτο μέχρι το σημείο που καταλήγει το τελευταίο
αυτό το τμήμα το ονομάζουμε άθροισμά τους:
Τη διαδικασία πολλαπλασιασμού δυο
τμημάτων o Wessel την περιγράφει ως εξής:
Πρώτον, τα
τμήματα πρέπει να έχουν τέτοιες διευθύνσεις ώστε και τα δυο να βρίσκονται στο
ίδιο επίπεδο με τη θετική μονάδα.
Δεύτερον,
σε ότι αφορά το μήκος, το γινόμενο θα έχει προς το ένα τμήμα τον ίδιο λόγο που
έχει το άλλο τμήμα προς τη μονάδα. (δηλαδή το μήκος του τμήματος-γινομένου θα
είναι ίσο με το γινόμενο των μηκών των τμημάτων-παραγόντων).
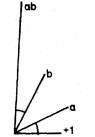 Τρίτον, αν μετατοπίσουμε τη θετική μονάδα,
τους παράγοντες και το γινόμενο σε μια κοινή αρχή; τότε το γινόμενο, σε ότι
αφορά τη διεύθυνσή του, Θα βρίσκεται στο ίδιο επίπεδο με τη μονάδα και τους
παράγοντες και Θα αποκλίνει από τον ένα παράγοντα τόσες μοίρες και προς το ίδιο
μέρος, όσο ο άλλος παράγοντας αποκλίνει από τη μονάδα- δηλαδή η γωνία
διεύθυνσης του γινομένου Θα
Τρίτον, αν μετατοπίσουμε τη θετική μονάδα,
τους παράγοντες και το γινόμενο σε μια κοινή αρχή; τότε το γινόμενο, σε ότι
αφορά τη διεύθυνσή του, Θα βρίσκεται στο ίδιο επίπεδο με τη μονάδα και τους
παράγοντες και Θα αποκλίνει από τον ένα παράγοντα τόσες μοίρες και προς το ίδιο
μέρος, όσο ο άλλος παράγοντας αποκλίνει από τη μονάδα- δηλαδή η γωνία
διεύθυνσης του γινομένου Θα
ισούται με το άθροισμα των γωνιών διεύθυνσης των παραγόντων.
Χρησιμοποιώντας αυτούς τους ορισμούς, ο Wessel έφτασε σε μια αναλυτική
έκφραση των προσανατολισμένων ευθύγραμμων τμημάτων του επιπέδου με τη βοή-θεια των μιγαδικών αριθμών, δίνοντας ταυτόχρονα μια ικανοποιητική γεωμετρική ερμηνεία στους τελευταίους.
Σ αυτήν την εργασία (και ορισμένες άλλες
που δημοσιεύτηκαν εκείνη την εποχή) υπάρχουν οι (βασικές ιδέες που συγκροτούν
σήμερα το υπόβαθρο του διανυσματικού λογισμού του επιπέδου: Η ουσιαστική όμως
ανάπτυξη του κλάδου αρχίζει μερικές δεκαετίες αργότερα, όταν οι ιδέες αυτές
γενικεύονται στον τρισδιάστατο χώρο.
Το 1843, ο W.R. Hamilton δημιούργησε τη Θεωρία των κβατερνίων
(quaternions), ενώ το 1844, ο Η. Grassmann, σε μια ακόμη πιο προχωρημένη
γενίκευση, παρουσίασε τη Θεωρία της επέκτασης (Ausdehnungslehre). Ο Hamilton χρησιμοποίησε
συστηματικά τους όρους κλιμακωτό ή βαθμωτό (scalar) για κάθε μέγεθος, «το οποίο
μπορεί να πάρει όλες τις τιμές της αριθμητικής κλίμακας (scale) από το αρνητικό
ως το Θετικό άπειρο», και διάνυσμα (vector) για κάθε ευθύγραμμο τμήμα
«με ορισμένο μήκος και ορισμένη διεύθυνση στο χώρο». Ο όρος vector, κατά μια
εκδοχή, προέρχεται από το λατινικό ρήμα vehere, που σημαίνει μεταφέρω. Ο
Grassmann επίσης χρησιμοποίησε τους όρους «εσωτερικό» και «εξωτερικό» γινόμενο.
Οι θεωρίες των κβατερνίων και της επέκτασης υπήρξαν σημαντικά βήματα στην
προσπάθεια αντιμετώπισης προβλημάτων, τόσο στα καθαρά Μαθηματικά όσο και στις
Φυσικές επιστήμες. Ο Hamilton, πριν επινοήσει τα κβατέρνια, είχε παρουσιάσει
σημαντικές έρευνες στην Οπτική και Δυναμική, ενώ στη συνέχεια ασχολήθηκε
εντατικά με τις εφαρμογές της νέας Θεωρίας. Επίσης, ο Grassmann, συνέλαβε τις
βασικές ιδέες της Θεωρίας του μελετώντας, από τη μια μεριά, την εμφάνιση των
αρνητικών αριθμών σε γεωμετρικά ζητήματα και, από την άλλη, προβλήματα της
Θεωρίας των παλιρροιών.
Η παραπέρα
εξέλιξη τον διανυσματικού λογισμού, που οδήγησε στην καθιερωμένη σήμερα μορφή
του, επηρεάστηκε αποφασιστικά από τις εξελίξεις στη Φυσική κατά το δεύτερο μισό
τον 19ου αιώνα. Η χρήση π.χ. της θεωρίας των κβατερνίων από τον J.C. Maxwell,
στο βιβλίο του «Πραγματεία πάνω στον Ηλεκτρισμό και Μαγνητισμό» (1874), οδήγησε
σε ορισμένες τροποποιήσεις, με βάση τις οποίες οι φυσικοί J.W. Gibbs και Ο. Heaviside,
δημιούργησαν στις αρχές της δεκαετίας του 1880 τη σύγχρονη θεωρία τον
διανυσματικού λογισμού. Τέλος, το 1888, ο G. Peano, με βάση τη Θεωρία της
επέκτασης του Grassmann, θεμελίωσε αξιωματικά την έννοια του διανυσματικού
χώρου.
Οι κωνικές τομές στην
αρχαiα Ελλάδα
Ο κύκλος, η παραβολή, η
έλλειψη και η υπερβολή λέγονται κωνικές τομές, γιατί μπορούν να
προκύψουν από την τομή μιας ορθής κωνικής επιφάνειας με ένα επίπεδο, το οποίο
δε διέρχεται από την κορυφή της. Η σημασία αυτών των καμπύλων φαίνεται ότι
αρχικά σχετίζονταν με ορισμένα προβλήματα γεωμετρικών κατασκευών, όπως για
παράδειγμα το περίφημο πρόβλημα διπλασιασμού του κύβου.( Για την ιστορική παράδοση του προβλήματος
θα γνωρίσουμε στο μάθημα). Δηλαδή, δοθέντος ενός κύβου, να κατασκευαστεί
ένας άλλος με διπλάσιο όγκο. Με αλγεβρικό συμβολισμό, αυτό σημαίνει ότι αν α
είναι η πλευρά του αρχικού κύβου, να κατασκευαστεί ένα ευθύγραμμο τμήμα x που Θα είναι η
πλευρά του κύβου με όγκο ![]() δηλ
δηλ![]() .
.
Ο Ιπποκράτης ο Χίος
(περ. 430 π.Χ.) ήταν ο πρώτος που ανήγαγε αυτό πρόβλημα στην κατασκευή δύο
τμημάτων x και y, τέτοιων ώστε ![]()
(κατασκευή δυο μέσων
αναλόγων - από αυτές τις σχέσεις εύκολα προκύπτει
![]() ).
).
Υπενθυμίζουμε
εδώ το πρόβλημα κατασκευής μιας μέσης αναλόγου, δηλ. ενός τμήματος
x τέτοιου ώστε ![]() , όπου α,β γνωστά ευθύγραμμα τμήματα. Αυτό το πρόβλημα
λύνεται εύκολα με κανόνα και διαβήτη, δηλ. με τη βοήθεια ευθείας και κύκλου.
Δεν συμβαίνει όμως το ίδιο με το πρόβλημα της κατασκευής δύο μέσων αναλόγων, το
οποίο απαιτεί τη χρησιμοποίηση διαφορετικών γεωμετρικών καμπύλων και οργάνων.
, όπου α,β γνωστά ευθύγραμμα τμήματα. Αυτό το πρόβλημα
λύνεται εύκολα με κανόνα και διαβήτη, δηλ. με τη βοήθεια ευθείας και κύκλου.
Δεν συμβαίνει όμως το ίδιο με το πρόβλημα της κατασκευής δύο μέσων αναλόγων, το
οποίο απαιτεί τη χρησιμοποίηση διαφορετικών γεωμετρικών καμπύλων και οργάνων.
Μια από τις
πολλές λύσεις που δόθηκαν κατά την αρχαιότητα είναι και του Μεναίχμου
(περ. 350 π.Χ.) με τη βοήθεια των κωνικών τομών.
Η λύση του
Μεναίχμου περιγράφεται με σύγχρονο αλγεβρικό συμβολισμό, ως εξής:
 Από
τις
Από
τις ![]() προκύπτει ότι
προκύπτει ότι ![]() (2) και
(2) και ![]() ή
ή ![]() (3) και επομένως τα μήκη των τμημάτων x,y μπορούν να
Θεωρηθούν ως οι συντεταγμένες του κοινού σημείου Μ των καμπύλων με εξισώσεις
(2) και (3), που είναι αντίστοιχα μια παραβολή και μια υπερβολή.
(3) και επομένως τα μήκη των τμημάτων x,y μπορούν να
Θεωρηθούν ως οι συντεταγμένες του κοινού σημείου Μ των καμπύλων με εξισώσεις
(2) και (3), που είναι αντίστοιχα μια παραβολή και μια υπερβολή.
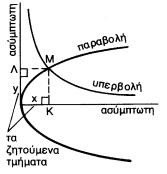
Στη γεωμετρική
κατασκευή τον Μεναίχμου, τα τμήματα x,y κατασκευάζονται με τη βοήθεια των προβολών
του σημείου τομής των 2 καμπύλων πάνω στις ασύμπτωτες της υπερβολής (η μια από τις οποίες είναι ταυτόχρονα και
άξονας συμμετρίας της παραβολής), αφού πρώτα κατασκευαστούν, σημείο προς
σημείο, οι καμπύλες σύμφωνα με τα γεωμετρικά ισοδύναμα των (2) και (3). Το Μ,
π.χ. ως σημείο της παραβολής προσδιορίζεται έτσι ώστε το τετράγωνο πλευράς ΜΚ
να είναι ισοδύναμο προς ένα ορθογώνιο με πλευρές 2α και ΜΛ (δηλαδή ![]() ), ενώ ως σημείο της υπερβολής προσδιορίζεται έτσι ώστε το
ορθογώνιο με πλευρές ΜΛ και ΜΚ να είναι ισοδύναμο προς ένα ορθογώνιο με πλευρές
2α και α (δηλ.
), ενώ ως σημείο της υπερβολής προσδιορίζεται έτσι ώστε το
ορθογώνιο με πλευρές ΜΛ και ΜΚ να είναι ισοδύναμο προς ένα ορθογώνιο με πλευρές
2α και α (δηλ. ![]() ).
).
Αυτή είναι η πρώτη γνωστή εμφάνιση των κωνικών
τομών στα αρχαία ελληνικά μαθηματικά- πρέπει όμως να τονιστεί ότι τόσο ο όρος «κωνική
τομή», όσο και οι ειδικότερες ονομασίες «παραβολή», «έλλειψη» και
«υπερβολή» είναι μεταγενέστερες του Μεναίχμου.
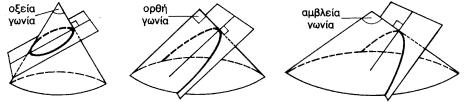
Οι καμπύλες αυτές, γύρω στο 300 π.Χ. ταυτίστηκαν για πρώτη φορά
με τις τομές που δημιουργούνται στην επιφάνεια ενός κώνου από ένα επίπεδο
κάθετο σε μια γενέτειρά του. Ανάλογα με τη γωνία της κορυφής του κώνου, οι
καμπύλες αυτές ορίστηκαν ως «οξυγωνίου κώνου τομή» (έλλειψη), «ορθογωνίου κώνου
τομή» (παραβολή) και «αμβλυγωνίου κώνου τομή» (υπερβολή).
Οι όροι αυτοί χρησιμοποιούνται από τον Αρχιμήδη (287-212 π.Χ.) στα έργα τον «Τετραγωνισμός ορθογωνίου κώνου τομής» και «Περί κωνοειδών και σφαιροειδών»
Οι νέοι ορισμοί
έδωσαν τη δυνατότητα μιας
Θεωρητικής μελέτης των τριών καμπύλων, με αποκορύφωμα τα περίφημα «Κωνικά» του
Απολλώνιου (περ. 250 π.Χ.). Το έργο αυτό ήταν χωρισμένο σε 8 βιβλία που
περιείχαν μια άψογη γεωμετρική Θεωρία των κωνικών τομών και ένα ανεξάντλητο
πλήθος νέων αποτελεσμάτων. Στα 7 πρώτα βιβλία που έχουν διασωθεί υπάρχουν 387
θεωρήματα ενώ στο 8ο, κατά μαρτυρία τον Πρόκλου, υπήρχαν άλλα 100. Μια βασική
καινοτομία του Απολλώνιου υπήρξε ο ορισμός των τριών καμπύλων μέσω τριών
διαφορετικών τομών ενός μόνο κώνου καθώς και η εισαγωγή των όρων «παραβολή»,
«έλλειψη» και «υπερβολή».
Τα ονόματα αυτά έχουν άμεση σχέση με το τρόπο ορισμού των κωνικών τομών που εισήγαγε
ο Απολλώνιος, σύμφωνα με τον οποίο, σε κάθε τομή του πλευρά την κάθετη κώνου
από το επίπεδο αντιστοιχεί ένα σταθερό μήκος (παράμετρος). Ο Απολλώνιος έδειξε
ότι για κάθε καμπύλη, τα γραμμοσκιασμένα εμβαδά σε καθένα από τα παρακάτω
σχήματα είναι ίσα μεταξύ τους. Το ένα από αυτά είναι το τετράγωνο με πλευρά την
κάθετη y από ένα σημείο της καμπύλης προς τον άξονα συμμετρίας της- το άλλο είναι
ένα ορθογώνιο, με μια πλευρά την απόσταση x του ίχνους αυτής της κάθετης από
την κορυφή της καμπύλης. Η σχέση της άλλης πλευράς του ορθογωνίου προς τη
σταθερή παράμετρο της τομής είναι αυτή που καθορίζει τη μορφή και το όνομα της
καμπύλης. Αν η άλλη πλευρά ισούται («παραβάλλεται») προς την παράμετρο, τότε η
καμπύλη είναι μια παραβολή. Όταν η άλλη πλευρά είναι μικρότερη («ελλείπει») από
την παράμετρο, η καμπύλη είναι μια
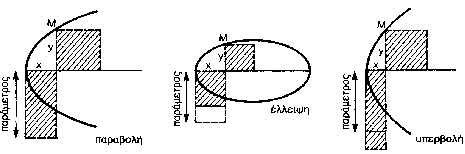
έλλειψη, ενώ όταν είναι μεγαλύτερη
(«υπερβάλλει»), η καμπύλη είναι μια
υπερβολή.
Η μελέτη
των κωνικών τομών στην αρχαία Ελλάδα, όπως κυρίως εμφανίζεται στα «Κωνικά», εντάσσεται μέσα στο γενικότερο
πλαίσιο μελέτης των μαθηματικών που
έδινε έμφαση στο θεωρητικό ενδιαφέρον και όχι στις πρακτικές εφαρμογές. Ο ίδιος ο Απολλώνιος, στους προλόγους του 4ου και 5ου βιβλίου, επισημαίνει
ότι η αξία του έργου του βρίσκεται στα
θεωρήματα αυτά καθε αυτά και τα κίνητρα που δίνουν για νέες έρευνες.
Οι
κωνικές τομές στη νεώτερη εποχή
Η μελέτη των κωνικών τομών συνεχίστηκε από τους Άραβες και ιδιαίτερα τους Ευρωπαίους μαθηματικούς της Αναγέννησης. Από καθαρά μαθηματική άποψη, η πλέον ουσιαστική εξέλιξη υπήρξε η εφαρμογή αλγεβρικών μεθόδων που οδήγησε βαθμιαία στην αποδέσμευση αυτών των καμπύλων από τον κώνο και στον ορισμό τους ως γεωμετρικών τόπων σημείων, οι συντεταγμένες των οποίων ως προς ένα σύστημα σνντεταγμένων ικανοποιούν μια εξίσωση 2ου βαθμού με 2 μεταβλητές.
Εκείνο
όμως που χαρακτηρίζει ιδιαίτερα τη νεώτερη εποχή είναι οι πολλές εφαρμογές των κωνικών τομών σε διάφορους
κλάδους της επιστήμης, της τέχνης και
της τεχνολογίας.
Στην
αστρονομία ο Kepler, με το έργο του "Astronomia nονa" (1609), έδωσε μια απλή ερμηνεία της κίνησης των πλανητών,
αντικαθιστώντας το πολύπλοκο σύστημα
των κυκλικών κινήσεων με ελλειπτικές τροχιές. Συγκεκριμένα, ο πρώτος
νόμος του Kepler αναφέρει ότι: «Οι
τροχιές των πλανητών είναι ελλείψεις, στη μία εστία των οποίων βρίσκεται ο ήλιος».
Η έλλειψη χρησιμοποιήθηκε επίσης στη ζωγραφική για την προοπτική
αναπαρά-σταση του κύκλου, γεγονός που οδήγησε στην επινόηση νέων μεθόδων
κατασκευής της από ζωγράφους της Αναγέννησης.
Σημαντικές επίσης υπήρξαν οι εφαρμογές των
κωνικών τομών στον αρχιτεκτονικό σχεδιασμό μεγάλων έργων, όπως θόλους
εκκλησιών, γέφυρες κ.λπ.
Ένας άλλος τομέας
τον οποίο χρησιμοποιήθηκε η θεωρία των κωνικών τομών, ήταν η βαλλιστική και συγκεκριμένα το
πρόβλημα
καθορισμού της τροχιάς των βλημάτων. Με το πρόβλημα αυτό ασχολήθηκαν πολλοί επιστήμονες κατά το 16ο και 17ο αιώνα ο Γαλιλαίος,
χρησιμοποιώντας ιδιότητες που είχαν αποδειχθεί από τον Απολλώνιο στα «Κωνικά» απέδειξε Θεωρητικά το 1937 ότι η
τροχιά ενός βλήματος είναι
παραβολή.
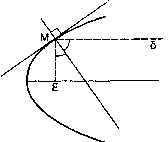 Μια άλλη ιδιότητα της παραβολής,
γνωστή από την αρχαιότητα, έχει
αξιοποιηθεί από τη σύγχρονη τεχνολογία
στην κατασκευή τηλεσκοπίων και φανών. Αν μια ευθεία δ, παράλληλη προς τον άξονα
συμμετρίας της παραβολής, τέμνει την παραβολή στο Μ. τότε η κάθετη στην εφαπτομένη της παραβολής στο Μ διχοτομεί τη
γωνία που σχηματίζουν οι ευθείες δ και
ΜΕ (όπου Ε η εστία). Σύμφωνα με την ιδιότητα
αυτή και το νόμο της ανάκλασης, οι φωτεινές ακτίνες που προέρχονται από
μια απομακρυσμένη πηγή, όπως π.χ. ένα αστέρι (και είναι επομένως σχεδόν
παράλληλες), μετά την ανάκλασή τους σε μια παραβολική επιφάνεια στραμμένη προς
την πηγή θα συγκεντρωθούν γύρω από την εστία. Η συγκέντρωση αυτή έχει ως
αποτέλεσμα τη σημαντική ενίσχυση ασθενών φωτεινών σημάτων. Αντίστροφα, η
τοποθέτηση μιας φωτεινής πηγής στην εστία παραβολικής επιφάνειας έχει ως
αποτέλεσμα τη δημιουργία μιας δέσμης παράλληλων ακτίνων.
Μια άλλη ιδιότητα της παραβολής,
γνωστή από την αρχαιότητα, έχει
αξιοποιηθεί από τη σύγχρονη τεχνολογία
στην κατασκευή τηλεσκοπίων και φανών. Αν μια ευθεία δ, παράλληλη προς τον άξονα
συμμετρίας της παραβολής, τέμνει την παραβολή στο Μ. τότε η κάθετη στην εφαπτομένη της παραβολής στο Μ διχοτομεί τη
γωνία που σχηματίζουν οι ευθείες δ και
ΜΕ (όπου Ε η εστία). Σύμφωνα με την ιδιότητα
αυτή και το νόμο της ανάκλασης, οι φωτεινές ακτίνες που προέρχονται από
μια απομακρυσμένη πηγή, όπως π.χ. ένα αστέρι (και είναι επομένως σχεδόν
παράλληλες), μετά την ανάκλασή τους σε μια παραβολική επιφάνεια στραμμένη προς
την πηγή θα συγκεντρωθούν γύρω από την εστία. Η συγκέντρωση αυτή έχει ως
αποτέλεσμα τη σημαντική ενίσχυση ασθενών φωτεινών σημάτων. Αντίστροφα, η
τοποθέτηση μιας φωτεινής πηγής στην εστία παραβολικής επιφάνειας έχει ως
αποτέλεσμα τη δημιουργία μιας δέσμης παράλληλων ακτίνων.