ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ

 Εξεταστική Περίοδος Σεπτεμβρίου 2002

Τμήμα Μαθηματικών

 Καρλόβασι  12 /09/ 2002

                

 

 

Θέματα στην Αναλυτική Γεωμετρία

 

  1. Δείξτε με εργαλεία  της Αναλ. Γεωμετρίας ότι οι διαγώνιοι ενός παραλληλογράμμου τέμνονται κάθετα αν και μόνο αν το παραλληλόγραμμο είναι ρόμβος. Εφαρμογή: Δείξτε ότι η κορυφή και τα μέσα τριών πλευρών ενός ισοσκελούς τριγώνου είναι  κορυφές ενός ρόμβου.

  2. Δίνεται το τρίγωνο με πλευρές τις ευθείες x + y = 2, x – y = 0, 2x – y = 4.
    Βρείτε το κέντρο του εγγεγραμμένου κύκλου του τριγώνου καθώς και το ορθόκεντρό του.

  3. Θέλουμε να κατασκευάσουμε ένα τούνελ πλάτους 20 m μέσα από ένα βουνό έτσι ώστε η εγκάρσια τομή του να έχει σχήμα (αντεστραμμένης) παραβολής. Απαιτούμε για οικονομικούς λόγους, το τούνελ να έχει το ελάχιστο δυνατό ύψος ώστε να περνά ίσα – ίσα ένα ιδεατό φορτηγό σε σχήμα  κύβου ύψους 10 m.  Βρείτε την εξίσωση της παραβολής και το ύψος του τούνελ.

  4. Κάντε κατάλληλη στροφή του συστήματος αξόνων 0xy ώστε να εξαφανιστεί ο μεικτός όρος xy  της καμπύλης με εξίσωση 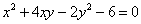 στο νέο σύστημα αξόνων Οx’y’. Δείτε στη συνέχεια ποια καμπύλη παριστάνει η αρχική εξίσωση.

  5. Να βρεθεί η εξίσωση του επιπέδου που διέρχεται από το σημείο Α και είναι παράλληλο στις ευθείες ε1 και ε2 όπου  Α(1,2,-1),

                   & .

 

 

Τα θέματα είναι ισοδύναμα. Καλή επιτυχία!

 

Ο διδάξας Χαρ. Κορνάρος