ΑΣΚΗΣΕΙΣ ΠΡΟΤΑΣΙΑΚΗΣ ΛΟΓΙΚΗΣ
1. Δίνονται οι ατομικές προτάσεις :
Α1 : " ο 3 είναι πρώτος "
Α2 : " ο 3 διαιρεί το 15 "
Α3 : " ο 3 διαιρεί το 2 "
Α4 : " ο 3 διαιρεί το 12 "
α . Να δοθεί μια απονομή
αλήθειας ( οποιαδήποτε ) στις παραπάνω προτάσεις .
β . Να υπολογιστεί η
αντίστοιχη εκτίμηση W , που
επεκτείνει την παραπάνω
απονομή για την
πρόταση (Α1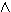 Α2)®(Α3
Α2)®(Α3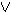 Α4)
Α4)
2 . Να δειχτεί ότι οι ακόλουθες προτάσεις είναι
ταυτολογίες :
α . 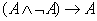 β .
β . 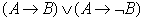
γ . 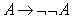 δ
.
δ
. 
3 . Aν Σ =
{A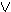 B , A®Γ } , να δειχτεί ότι Σ
B , A®Γ } , να δειχτεί ότι Σ
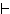 (Β
(Β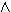 Γ)
Γ)

4 . Aν Σ = {A«Γ , Β«Δ , (A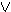 Β)
Β)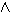 (Γ
(Γ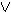 Δ) } , να δειχτεί ότι
Δ) } , να δειχτεί ότι
5 . Αν Σ1 και Σ2 είναι σύνολα
προτάσεων της Λ.Π (Λογικής των
προτάσεων ), να εξετάσετε ποιος από τους ακόλουθους ισχυρισμούς είναι αληθής και
ποιος ψευδής :
α . Συν(Σ1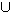 Σ2) = Συν(Σ1)
Σ2) = Συν(Σ1)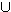 Συν(Σ2)
Συν(Σ2)
β . Συν(Σ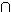 Σ2) =
Συν(Σ1)
Σ2) =
Συν(Σ1)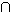 Συν(Σ2)
Συν(Σ2)
Σε περίπτωση που ο
αντίστοιχος ισχυρισμός είναι αληθής να δοθεί απόδειξη , ενώ αν δεν
είναι αληθής να δοθεί αντιπαράδειγμα .
6 . Δίνονται οι προτάσεις :
Α : " Το τετράπλευρο
ΚΛΜΝ είναι παραλληλόγραμμο "
Β : " Οι διαγώνιοι του
ΚΛΜΝ διχοτομούνται "
Γ : " Οι απέναντι
γωνίες του ΚΛΜΝ είναι ίσες "
Δ : " Οι απέναντι πλευρές
του ΚΛΜΝ είναι ίσες "
Να εξεταστεί αν το σύνολο Σ
= { Α , Α«Β , Α«Γ , Α®(Β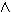 Δ) }
Δ) }
είναι συνεπές .
7 . Να δειχτεί με τη μέθοδο της δυαδικής
επίλυσης ότι τα ακόλουθα σύνολα είναι μη επαληθεύσιμα :
a . Σ = { 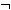 A
A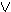 B
B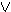 Δ ,
Δ , 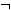 B
B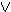 Δ
Δ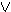 A ,
A , 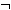 Δ
Δ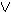 Γ ,
Γ , 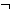 Δ
Δ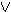 A , A
A , A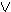 B , B
B , B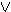 ØΓ
,
ØΓ
, 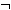 A
A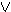
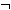 B }
B }
γ . Σ = { A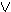 B
B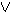 Γ, A
Γ, A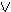 B
B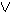
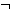 Γ , A
Γ , A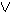
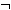 B ,
B , 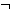 A
A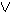
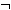 Γ ,
Γ , 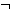 Α
Α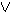 Γ }
Γ }
8 . Να δειχτεί με τη μέθοδο της δυαδικής
επίλυσης ότι :
α . {
Β®Α ,
îà ,
Δ®Β ,
Β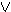 Γ
Γ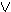 Δ }
Δ } 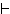 Α
Α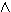 Β
Β
β .
{Α ®à ,
Α®Β
}
®à ,
Α®Β
} 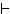 Α®Γ
Α®Γ
9 . Να γραφτούν οι ακόλουθες προτάσεις σαν
σύνολα προγραμματικών τύπων :
α .
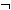 (Α
(Α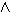 Β
Β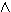
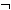 Γ)
Γ)
β .
Α«(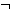 Β
Β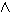
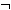 Γ)
Γ)
![]() Α2)®(Α3
Α2)®(Α3![]() Α4)
Α4)![]() β .
β . ![]()
![]() δ
.
δ
. ![]()
![]() B , A®Γ } , να δειχτεί ότι Σ
B , A®Γ } , να δειχτεί ότι Σ
![]() (Β
(Β![]() Γ)
Γ) ![]()
![]() Β)
Β)![]() (Γ
(Γ![]() Δ) } , να δειχτεί ότι
Δ) } , να δειχτεί ότι