Περίληψη στη Λογική των Προτάσεων. Ακαδημαικό έτος 2001 - 2002

Λογική των Προτάσεων

Α Μερος. Λογική των Προτάσεων.

Για να γράψουμε μια ατομική πρόταση ή μιά πιό σύνθετη χρησιμοποιούμε κάποια σύμβολα και κάποιο συντακτικό για να χειριζόμαστε σωστά τα σύμβολα. Ετσι μια οποιαδήποτε τυπική γλώσσα(γλώσσα εννούμε φυσικά ένα σύνολο συμβόλων όπως για παράδειγμα τα γράμματα μιας γραφομηχανής)αποτελείται από

• προτασιακά σύμβολα (κεφαλαία γράμματα Α,Β,.... που μπορούμε να φανταστούμε ότι παριστάνουν τις ατομικές προτάσεις δηλ. τα "ατομα" που μέσα τους δεν περιέχουν πιο απλή πρόταση) Επειδή επιτρέπονται και δείκτες π.χ Α₁ κοκ. υποθέτουμε βασικά ότι έχουμε άπειρα ατομικά σύμβολα!
• σύμβολα λογικών συνδέσμων(όπως σύμβολο διάζευξης, σύζευξης, άρνησης κ.οκ.χωρίς αυτά είναι εντελώς αδύνατον να φτιάξουμε σύνθετες προτάσεις) και τέλος
• κόμματα και παρενθέσεις , (, ) Με αυτά οριοθετούμε το τέλος και την αρχή μιας οποιαδήποτε πρότασης ή υποπρότασης .

Κάποιοι όμως τύποι δεν είναι προτάσεις διότι δεν ικανοποιούν κάποιους συντακτικούς κανόνες. Γιά παράδειμα ο τύπος ( δεν είναι ακριβώς μια πρόταση σαν τις άλλες διότι της λείπει μια παρένθεση δεξιά δηλ. η ) και πρέπει να  προστεθεί αν θέλουμε μια  να έχουμε μια κανονική πρόταση...Πρέπει λοιπον να ορίσουμε κάποιους συντακτικούς κανόνες. Το σύνολο των κανόνων αυτών αποτελεί  το συντακτικό της τυπικής μας γλώσσας.Τέλος για να έχουν κάποιο λογικό  νόημα(σημασία) οι προτάσεις μας πρέπει να δώσουμε καταρχήν κάποια απονομή αλήθειας στα ατομικά σύμβολά μας και με βάση κάποιους επαγωγικούς κανόνες να ορίσουμε την αλήθεια για μιά οποιαδήποτε σύνθετη πρόταση.. Π.χ ας υποθέσουμε ότι με Α συμβολίζουμε το άτομο "σήμερα βρέχει" και ας του απονέμουμε την τιμή α (δηλ. αλήθεια). Τότε είμαστε αναγκασμένοι να εκτιμήσουμε(να δώσουμε τιμή) την σύνθετη πρόταση "σήμερα δεν βρέχει" με την τιμή ψ(ψέμα). Συνοπτικά λοιπόν αναφέρουμε τα πιο σημαντικά πράγματα που αναφέραμε στην Θεωρία:

• κάθε απονομή(ή αποτίμηση) αλήθειας F στους ατομικούς τύπους μπορεί να επεκταθεί με φυσιολογικό τρόπο σε μια εκτίμηση αλήθειας V για τις σύνθετες προτάσεις της τυπικής μας γλωσσας.
• δεν υπάρχει μονάχα μια αποτίμηση. Θα λέγαμε μάλιστα ότι υπάρχουν άπειρες και όλες διαφορετικές μεταξύ τους διότι άπειρα είναι και τα ατομικά σύμβολα και άρα δυο αποτιμήσεις που διαφωνούν σε μια η περισσότερες ατομικές προτάσεις είναι διαφορετικές!  Όμως αν τύχει δυο αποτιμήσεις να συμφωνούν στις τιμές αλήθειας(α ή ψ)που δίνουν σε κάποια άτομα (πχ στα τρία  πρώτα Α, Β, Γ) τότε θα δίνουν την ίδια τιμή και σε οποιαδήποτε άλλη πρόταση που περιέχει μόνο τα Α, Β, Γ άτομα και κανένα άλλο.

Είδη των Προτάσεων

Με βάση τις εκτιμήσεις αλήθειας έχουμε χωρίσει τις προτάσεις της γλώσσας μας σε:

• λογικά αληθινές (ή ταυτολογίες) εάν επαληθεύονται από κάθε εκτίμηση
• επαληθεύσιμες όταν επαληθεύονται από κάποιες εκτιμήσεις μππορεί όμως όχι απ'όλες
• λογικά ψευδής(ή αντιλογίες) εάν δεν επαληθεύονται από καμμιά εκτίμηση.

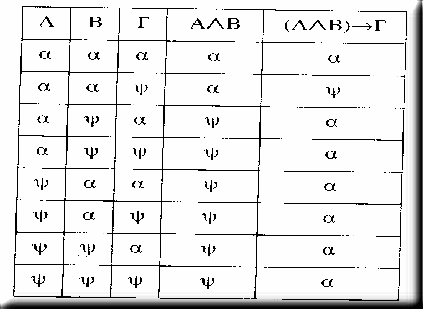
Για παράδειγμα η πρόταση Κ:   είναι επαληθεύσιμη διότι μια οποιαδήποτε εκτίμηση αλήθειας V με V(A)=α, V(Β)=α, και V(Γ)=ψ V(Δ)=ψ επαληθεύει την πρόταση δηλ. V(Κ)=α.

  Οι αληθοπίνακες αποτελούν ένα απλό τρόπο να καταγράφουμε όλες τις αποτιμήσεις αλήθειας για μιά δοθείσα πρόταση. Π.χ ο αληθοπίνακας της προτασης  είναι ο παρακάτω:

  Υπάρχουν μερικές ταυτολογίες που τις χρησιμοποιούμε αρκετά συχνά.

Αναφέρουμε για παράδειγμα τους νόμους του De Morgan, τον νόμο της Διπλής άρνησης, τον νόμο της άρνησης κοκ. Όταν λέμε νόμο εννοούμε μια πολύ χρήσιμη ταυτολογία. Με αληθοπίνακες μπορούμε να δείξουμε τους παρακάτω νόμους της λογικής των Προτάσεων:

  Μιά σπουδαία έννοια της Λογικής είναι και η έννοια της συνέπειας. Στην καθημερινή μας ζωή λέμε π.χ αν δεν διαβάζεις, αν δεν παρακολουθείς τα μαθήματα αν... και αν... τότε αυτό θα έχει ως συνέπεια να μην περάσεις το μάθημα κοκ. με το ίδιο ακριβώς τρόπο ορίζουμε την έννοια της συνέπειας και στη Προτασιακή Λογική. Έστω λοιπόν Σ ένα σύνολο προτάσεων. Θα λέμε οτι το Σ έχει ως (ταυτολογική)συνέπεια την πρόταση σ (και γράφουμε εάν για κάθε εκτίμηση αληθείας V η οποία επαληθεύει το Σ (δηλ. επαληθεύει κάθε πρόταση που ανήκει στις υποθέσεις Σ) τότε επαληθεύει και την σ (δηλ. V(σ)=α). Με χρήση αληθοπινάκων είναι πολύ εύκολο να ελένξουμε αν πράγματι αυτό συμβαίνει απλώς φτιάχνοντας ένα αληθοπίνακα με όλες τις προτάσεις του Σ και το σ και ελέγχοντας αν στις γραμμές που αληθευονται οι προτάσεις του Σ αληθεύει και η σ. Με Συν(Σ) εννούμε όλες τις προτάσεις που το Σ έχει συνέπεια.

Μια άλλη σημαντική έννοια είναι η έννοια του πότε ένα σύνολο Σ είναι συνεπές δηλ. επαληθεύσιμο. Είναι νομίζω φανερό από τον ορισμό ότι ένα ασυνεπές σύνολο είναι τόσο τρομερό ώστε να μπορεί να έχει ως συνέπεια του μια οποιαδήποτε πρόταση ακόμα και αντίφαση!! (Αυτό συμβαίνει και με τους ασυνεπείς ανθρώπους... δεν μπορείς να βασίζεσαι)

Με Ερμ(Σ) συμβολίζουμε το σύνολο όλων των εκτιμήσεων αληθείας που επαληθεύουν κάθε πρόταση του Σ. Ισχύουν αρκετές ιδιότητες σχετικά με Συν(Σ) και Ερμ(Σ).

Χρησιμοποιώντας τους νόμους που αναφέραμε προηγουμένως μπορούμε να φέρουμε μια οποιαδήποτε πρόταση σε Διαζευκτική Κανονική Μορφή(ΔΚΜ) και σε Συζευκτική Κανονική Μορφή(ΣΚΜ). Η ΔΚΜ είναι διάζευξη ή διαζεύξεις συζεύξεων  στοιχειωδών προτάσεων. Κατ'αρχην με στοιχειώδη πρόταση  εννούμε μια ατομική πρόταση ή μια άρνηση ατομικής πρότασης. Έτσι μια πρόταση της μορφής

είναι σε ΔΚΜ ενώ η ΣΚΜ έχει μέσα στις παρενθέσεις τις διαζεύξεις και απ'έξω τις συζεύξεις (σύζευξη διαζεύξεων). Αυτές οι μορφές χρησιμοποιούνται πάρα πολύ στην πράξη και θα πρέπει να έχουμε εξασκηθεί για να φέρνουμε κάθε πρόταση σε μια απ'τις παραπάνω μορφές. Να μερικές παρατηρήσεις:

Μπορούμε να χρησιμοποιήσουμε τους γνωστούς μας κανόνες και νόμους για να γράψουμε μια πρόταση σ σε ΔΚΜ και ΣΚΜ.
Παρ'ολα αυτά ίσως ο ευκολότερος τρόπος εάν μας ζητάνε την ΔΚΜ της σ είναι ο αληθοπίνακας της και συγκεκριμμένα οι γραμμές που δίνουν αλήθεια στην σ. Εάν μας ζητάνε την ΣΚΜ μπορούμε να χρησιμοποιήσουμε τον αληθοπίνακα της .
Η άρνηση μιας ΔΚΜ είναι μία πρόταση σε ΣΚΜ και η άρνηση μιας ΣΚΜ είναι μία πρόταση σε ΔΚΜ. Στην εφαρμοσμένη μαθηματική λογική χρησιμοποιείται κυρίως η ΣΚΜ. Συγκεκριμμένα κάθε πρόταση γράφεται πρώτα σε ΣΚΜ κια μετά ως σύνολο προγραμματικών τύπων όπως έχουμε αναφέρει στο μάθημα.

Για παράδειγμα η πρόταση

μπορεί να γραφεί ως σύνολο προγραμματικών τύπων ώς:

.

Φυσικά επειδή υπάρχει το και το μπορύμε να κάνουμε δυαδική επίλυση του δηλ. να σβήσουμε μια εμφάνιση του Β και μία του , έτσι προκύπτει ώς συνέπεια ο προγραμματικός τύπος

δηλ. η πρόταση  

Προσοχή δεν μπορούμε να κάνουμε επίλυση ενός ατόμου με την άρνησή του όταν βρίσκονται μέσα στον ίδιο προγραμματικό τύπο! (διότι π.χ το δεν αποτελεί σύγκρουση αλλα ταυτολογία). Επίσης στο παραπάνω παράδειγμα θα μπορούσαμε να κάμουμε επίλυση και ως προς D. Εξαρτάται πάντα από το τι θέλουμε να αποδείξουμε. Ας δώσουμε ένα ορισμό.

Ορισμός Έστω Σ ενα σύνολο προγραμματικών τύπων και σ μια πρόταση σε ΣΚΜ δηλ. ειναι γραμμένη ως σύζευξη των προγραμματικών τύπων C₁, C₂, ..., C_n . Γράφουμε και λέμε ότι η σ είναι απόδειξη με επίλυση από το Σ, εαν για κάθε προγραμματικό τύπο C_i της σ, υπάρχει μια απόδειξη με επίλυση απο το Σ της οποίας ο τελευταίος προγραμματικός τύπος της είναι ο C_i.

Μια ιδιαίτερη περίπτωση είναι εκείνη στην οποία μετά από επίλυση προκύπτει το κενό! Για παράδειγμα εάν έχουμε ένα σύνολο προτάσεων Σ  (σε ΣΚΜ) και κατά την πορεία μιας επίλυσης προκύψουν οι τύποι τότε θα επακολουθήσει επίλυση και θα προκύψει το κενό {} που το συμβολίζουμε και με ένα τετράγωνο □ και συμβολικά □ και εννούμε ότι το Σ είναι αντιφατικό. Για να είμαστε πιο αυστηροί μπορούμε να αποδείξουμε τα παρακάτω δυο σπουδαιότατα Θεωρήματα:

Θεώρημα της ορθότητας της μεθόδου της δυαδικής επίλυσης: Εάν □  τότε το Σ είναι ασυνεπές(δηλ. εάν προκύψει κενό κατά την επίλυση τότε κάθε παραπέρα προσπάθεια είναι χαμένη το Σ είναι ασυνεπές δηλ. άχρηστο!)
Θεώρημα της πληρότητας της μεθόδου της επιλυσης: Εάν το Σ είναι ασυνεπές τότε σίγουρα θα το ανακαλύψεις και με επίλυση δηλ. έχουμε πληρότητα της μεθόδου...

Τώρα που μιλάμε για ασυνεπές σύνολο να δώσουμε το περίφημο Θεώρημα του Συμπεράσματος που λέει για οποιοδήποτε Σ και σ, τ προτάσεις ότι:

εάν και μόνον εάν

φυσικά αντί μπορούμε να βάλουμε . Οπότε εάν εφαρμόσουμε το Θεώρημα του συμπεράσματος για τ ισον με το □ δηλ. με οποιαδήποτε αντίφαση και σ με  τότε παίρνουμε μια χρήσιμη μέθοδο απόδειξης (με επίλυση) του απο το Σ, με απόδειξη  του □:

□

 Τελειώνουμε με μια άλλη  έννοια  απόδειξης μιας πρότασης δηλ. της απόδειξης χρησιμοποιώντας αξιωματικές μεθόδους. Είναι γνωστό ότι όλες οι σοβαρές επιστήμες στηρίζoνται σε κάποια αξιωματικά πλαίσια. και μεθόδους, πάρτε για παράδειγμα την Ευκλείδιο Γεωμετρία.Υπάρχουν εδώ κάποιες προτάσεις που τις έχουμε δεχτεί ώς αληθινές χωρίς να μας γνοιάζει αν ίσως σε κάποια αποτίμηση δεν αληθεύουν! Τις έχουμε δεχθεί απόλυτα δηλ. ως αξιώματα. Τις χρησιμοποιούμε με κάποιους συλλογιστικούς κανόνες(κανόνες παραγωγής νέων προτάσεων) και αποδεικνύουμε θεωρήματα(δηλ. προτάσεις που έπονται από τα αξιώματα και όχι κατανάγκη προτάσεις που είναι ταυτότητες ή ταυτολογίες!). Κάτι τέτοιο κάνουμε και στην αξιωματική μέθοδο δηλ:

Θέτουμε κάποια αξιώματα (προτάσεις) που ουσιαστικά είναι κάποιοι σπουδαίοι λογικοί νόμοι για κάποιους συνδέσμους. Π.χ  
• 
• 
• 
Στην συνέχεια θέτουμε κάποιους κανόνες παραγωγής νέων προτάσεων π.χ χρησιμοποιούμε τον κανόνα της απόθεσης Modus Ponens (MP) o οποίος μας βεβαιώνει ότι από τις μπορούμε να συμπεράνουμε την πρόταση .

Θα πρέπει να τονίσουμε οτι τα αξιώματα δεν είναι πεπερασμένα αλλά άπειρα το πλήθος διότι με μπορούμε να θέσουμε οποιαδήποτε πρόταση στα παραπάνω άρα ουσιαστικά έχουμε ένα ολόκληρο σχήμα αξιωμάτων!

Ετσι λοιπον μπορούμε να ξεκινήσουμε να αποδεικνύουμε μια οποιαδήποτε πρόταση (που φυσικά περιέχει σύμβολα μόνο απο την γκάμα των αξιωμάτων μας - εδώ μόνο με και ). Π.χ μπορούμε να αποδείξουμε την ώς εξής: Θέτουμε στο α και β αξίωμα αντι το αντί το και αντι το και κάνουμε ΜΡ. Το αποτέλεσμα που βρίσκουμε το κάνουμε ξανά ΜΡ με το α αξίωμα όπου τώρα θέτουμε αντι το και αντι το .

Φυσικά έχουν προταθεί κατά καιρούς πολλά αξιωματικά συστήματα για να καλύψουν προτάσεις που περιέχουν και  άλλους συνδέσμους π.χ διαζεύξεις κοκ. Γενικά η απόδειξη με αξιώματα αν και είναι μηχανική διαδικασία χρειάζεται φαντασία ώστε να χρησιμοποιήσουμε τα κατάλληλα αξιώματα με τις κατάλληλες εφαρμογές ΜΡ. Ευτυχώς υπάρχουν κάποιες προτάσεις που μας λύνουν τα χέρια. Ομως ας δώσουμε κατ΄αρχήν ένα ορισμό.

Εστω Σ  ένα σύνολο προτάσεων και μια πρόταση. Θα λέμε ότι αυτή είναι (τυπικά)αποδείξιμη από το Σ με τα παραπάνω αξιώματα και τον παραπάνω αποδεικτικό κανόνα (και θα γράφουμε ) εάν υπάρχει απόδειξη με τελευταίο βήμα την και όλες οι ενδιάμεσες προτάσεις(τα ενδιάμεσα βήματα) να είναι είτε αξιώματα είτε κάποια πρόταση από το είτε προέρχεται από προηγούμενα βήματα της απόδειξης με εφαρμογή του ΜΡ.

Η σημαντική πρόταση που και εδώ ισχύει είναι το Θεώρημα του συμπεράσματος στην μορφή:

εάν και μόνον εάν .

Απότι ηδη έχετε καταλάβει οι έννοιες  είναι ισοδύναμες. Αυτό πράγματι ισχύει διότι  ισχύουν τα παρακάτω θεωρήματα ορθότητας και πληρότητας:

Θεώρημα της ορθότητας της αξιωματικής μεθόδου: Εάν σ  τότε το .(δηλ. εάν προκύψει με αξιώματα και το μια τυπική απόδειξη του σ τότε  η σ  είναι συνέπεια λογική του Σ).
Θεώρημα της πληρότητας της μεθόδου: Εάν το τότε σίγουρα θα προκύψει (ίσως μετά απο μία μέρα...) το σ με μια αξιωματική απόδειξη από το .

Τελειώνουμε  με το Θεώρημα της Συμπάγειας που το χρησιμοποιούμε και στην τοπολογία!

Θεώρημα της συμπάγειας: Ενα άπειρο σύνολο προτάσεων είναι ικανοποιήσιμο(δηλ. συνεπές) εάν και μόνον εαν κάθε πεπερασμένο υποσύνολό του είναι ικανοποιήσιμο!

Home