Εφαρμογές & Λογισμικό

Όπως εύκολα μπορεί να διαπιστώσει κάποιος μελετώντας τις παραπάνω εργασίες (αλλά και αντίστοιχες σημειώσεις) η κατάλληλη αγοραπωλησία συμβολαίων προαίρεσης βελτιώνει πολύ την αποτελεσματικότητα του χαρτοφυλακίου που τα περιέχει. Στην περίπτωση στην οποία δεν υπάρχουν διαθέσιμα τέτοια συμβόλαια στην αγορά τότε η κατασκευή χαρτοφυλακίου καταλήγει στην εφαρμογή της θεωρίας του Markowitz, επομένως η παραπάνω θεωρία είναι μια γενίκευση της θεωρίας του Markowitz (δείτε πρόβλημα (9) των διαφανειών Χρηματοοικονομικά Μαθηματικά Ι).

Συχνά, ολόκληρα εξαμηνιαία μαθήματα αλλά και ολόκληρα βιβλία (ακόμη και πρόσφατα) αναλώνονται στην αποτίμηση (κοστολόγηση) των συμβολαίων προαίρεσης και όχι στην σωστή εφαρμογή τους με αποτέλεσμα οι φοιτητές να μην είναι σε θέση να τα χρησιμοποιούν κατάλληλα. Όσον αφορά την αποτίμηση των συμβολαίων αυτών θα πρέπει να καταστεί σαφές ότι στην πράξη οι τιμές τους προκύπτουν σύμφωνα με τον νόμο της προσφοράς και ζήτησης αλλά και την παρουσία ευκαιριών σίγουρου κέρδους. Επομένως το μόνο που μπορούμε να κάνουμε θεωρητικά είναι να υπολογίσουμε το διάστημα τιμών (λύνοντας τα προβλήματα (10) και (11) των σημειώσεων) που δεν δημιουργούν ευκαιρία σίγουρου κέρδους προκειμένου να έχουμε μια τάξη μεγέθους της αξίας αυτού του συμβολαίου. Έτσι λοιπόν οι αντίστοιχες θεωρίες αποτίμησης δεν καταλήγουν (και ούτε πρόκειται να καταλήξουν ποτέ) σε μια τιμή πώλησης η οποία τελικά θα εμφανιστεί στην αγορά και άρα δεν έχουν κανένα πρακτικό ενδιαφέρον. Ένα επιχείρημα υπέρ του παραπάνω συμπεράσματος είναι ότι επειδή οι αξίες των συμβολαίων προαίρεσης εξαρτώνται από τις υποκείμενες μετοχές είναι αδύνατο να προβλέψεις την αξία τους χωρίς πρώτα να προβλέψεις την αξία των μετοχών.

Η θεωρία του Markowitz δεν λαμβάνει υπόψη τα διαθέσιμα συμβόλαια προαίρεσης και ως εκ τούτου δεν πραγματοποιεί μεταφορά ρίσκου με συνέπεια κάποιος να είναι υποχρεωμένος να μετρά τον κίνδυνο (Value at Risk) και όχι να τον διαχειρίζεται. Η μέτρηση όμως του κινδύνου δεν οδηγεί σε στατικά αποτελέσματα διότι η αγορά είναι δυναμική και επομένως την επόμενη κιόλας μέρα μπορεί να μεταβληθεί δραστικά η αντίστοιχη ποσότητα. Η διαχείριση κινδύνου όμως είναι κάτι στατικό και αντικειμενικό και είναι αυτό ακριβώς που προτιμούν οι επενδυτές. Σε πλήρη αντιστοιχία, στον Αναλογισμό και στην Ασφαλιστική επιστήμη, η μεταφορά ρίσκου γίνεται μέσω της έννοιας της αντασφάλισης. Επομένως ένας επαγγελματίας θα πρέπει να γνωρίζει τους διαθέσιμους τρόπους μεταφοράς ρίσκου και μέσω της επίλυσης ενός προβλήματος βελτιστοποίησης να καταλήξει στην κατάλληλη για αυτόν στρατηγική.

Ανάπτυξη Λογισμικού με Πρακτικό Ενδιαφέρον

Σκοπός μας είναι η ανάπτυξη λογισμικού με πρακτικό ενδιαφέρον το οποίο θα παραθέτουμε εδώ.

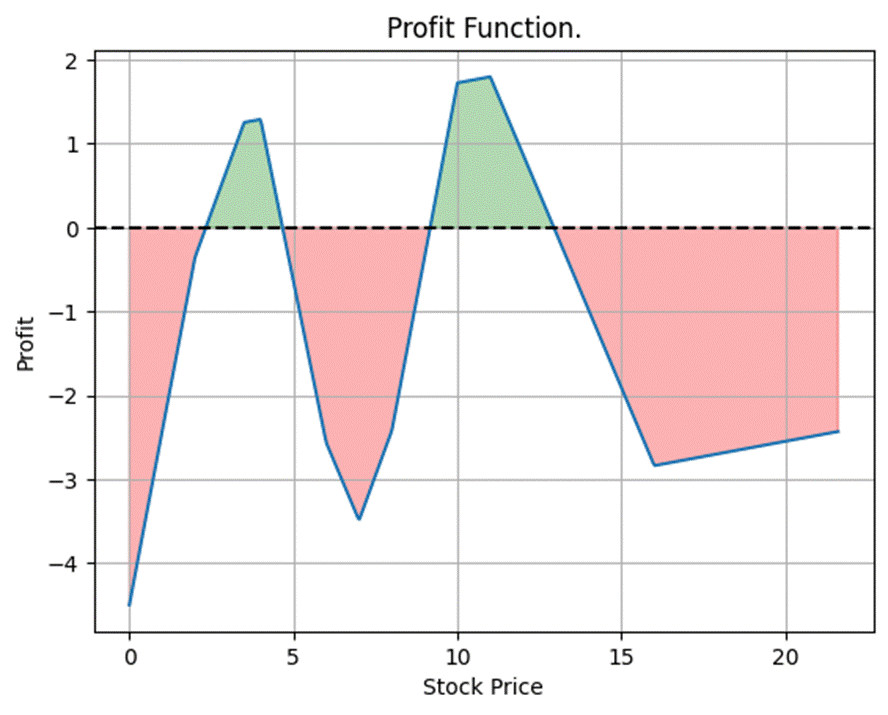
Δεδομένης μιας πρόβλεψης για το που θα βρεθεί η αξία μιας μετοχής μπορούμε εφοδιάζοντας το χαρτοφυλάκιο μας με κατάλληλα call και put options, να κατασκευάσουμε χαρτοφυλάκιο το οποίο να έχει κέρδος αν η πρόβλεψη επαληθευθεί, δείτε σχήμα παρακάτω. Για το σκοπό αυτό θα ήταν ιδιαίτερα χρήσιμο κατάλληλο λογισμικό προγνωστικού τύπου το οποίο να λαμβάνει υπόψη και τα πρόσφατα γεγονότα. Για να γίνει αυτό θα πρέπει παρελθοντικά αριθμητικά δεδομένα να συνδεθούν με γεγονότα της ίδιας εποχής οπότε σε αυτό η μηχανική μάθηση, τεχνητή νοημοσύνη κ.α. θα διαδραματίσουν σημαντικό ρόλο. Το παρακάτω σχήμα προέκυψε χρησιμοποιώντας πραγματικά δεδομένα (bid-ask spread) με αυτό τον κώδικα Python. Στο αρχείο αυτό θα βρείτε και τον αντίστοιχο κώδικα ο οποίος εντοπίζει, αν υπάρχει, ευκαιρία σίγουρου κέρδους δεδομένης μιας μετοχής και των call και put options.
Η θεωρία χαρτοφυλακίου κατά Markowitz λοιπόν έχει δυο σκέλη: το πρώτο είναι η πρόβλεψη του επενδυτή και το δεύτερο η κατασκευή του χαρτοφυλακίου με βάση αυτή την πρόβλεψη. Στο πρώτο σκέλος χρησιμοποιεί μόνο παρελθοντικά αριθμητικά δεδομένα και ως εκ τούτου είναι ελλιπής. Στο δεύτερο σκέλος δεν λαμβάνει υπόψη άλλα αγαθά τα οποία σχετίζονται με τις μετοχές, όπως τα call και put. Με την μεθοδολογία που αναπτύξαμε έχουμε βελτιώσει κατά πολύ το δεύτερο σκέλος της θεωρίας χαρτοφυλακίου οπότε με τη χρήση μηχανικής μάθησης και τεχνητής νοημοσύνης μένει να βελτιωθεί και το πρώτο σκέλος.
Έχουμε κατασκευάσει τον κατάλληλο κώδικα Python με τον οποίο κανείς μπορεί να εφαρμόσει τη θεωρία του Markowitz για όσες μετοχές θέλει. Λαμβάνει πραγματικά ιστορικά αριθμητικά δεδομένα για να υπολογίσει τις διακυμάνσεις και τις συνδιακυμάνσεις (Markowitz_Portfolio_Construction.zip).

Όσον αφορά την αποτίμηση συμβολαίων προαίρεσης (option pricing problem) μπορεί κανείς να χρησιμοποιήσει τον κώδικα Python (FairVauleOption) που υπάρχει στο ίδιο συμπιεσμένο αρχείο. Με αυτόν τον κώδικα μπορούμε να υπολογίσουμε το διάστημα χωρίς arbitrage της αξίας ενός συμβολαίου με συνάρτηση απολαβής f(x) η οποία δίνεται από τον χρήστη αλλά και την δίκαιη τιμή πώλησης υπό την έννοια της μέγιστης πιθανής ζημιάς. Προτείναμε και άλλους ορισμούς δίκαιων τιμών και ως εκ τούτου αποδεικνύεται ότι δεν υπάρχει μοναδική τέτοια τιμή ενώ στις περιπτώσεις όπου υπάρχει τότε θα είναι αυτή του ορισμού υπό την έννοια της μέγιστης πιθανής ζημιάς. Σημειώστε ότι η συνάρτηση απολαβής πρέπει να είναι τμηματικά γραμμική με πεπερασμένους κλάδους. Στον κώδικα αυτό χρησιμοποιούμε πραγματικά δεδομένα (bid-ask spread) και μπορεί να εφαρμοσθεί στην πράξη για την τιμολόγηση ενός οποιουδήποτε παραγώγου γραμμένου σε μια μετοχή σε αντίθεση με τα γνωστά μοντέλα τιμολόγησης Black-Scholes, Binomial κ.α. Μπορεί κανείς να δοκιμάσει την τιμολόγηση ενός απλού call option δεδομένου ότι υπάρχουν άλλα call και put στην αγορά τόσο με την παραπάνω τεχνική όσο και με τις γνωστές τεχνικές τιμολόγησης. Πουλώντας/αγοράζοντας ένα συμβόλαιο σε κάποια τιμή ο πωλητής/αγοραστής μπορεί να κατασκευάσει κατάλληλο αντισταθμιστικό χαρτοφυλάκιο ανάλογα με τις προβλέψεις του (δείτε κώδικες WriterhedgingOption1 και BuyerHedgingOption1). Έχουμε κατασκευάσει τον κατάλληλο κώδικα Python ο οποίος υπολογίζει την δίκαιη τιμή κατά Black-Scholes οποιουδήποτε συμβολαίου γραμμένου σε μια μετοχή. Λαμβάνει πραγματικά ιστορικά αριθμητικά δεδομένα για να υπολογίσει την μεταβλητότητα (Black_Scholes_Fair_Price.zip). Παρομοίως με το διωνυμικό μοντέλο (BinomialModel.zip).
Ένα άλλο σημαντικό θέμα των χρηματοοικονομικών μαθηματικών είναι οι δυναμικές συναλλαγές. Έχουμε προτείνει μια τέτοια διαδικασία η οποία στηρίζεται στην αρχή «αγόρασε φθηνά-πούλα ακριβά» και στηρίζεται σε μια πρόβλεψη που αφορά περισσότερο την μελλοντική διακύμανση της αξίας της μετοχής. Ένας τέτοιος τρόπος πρόβλεψης είναι μέσω Στοχαστικών Διαφορικών Εξισώσεων, δείτε παρακάτω. Σκοπός μας στη συνέχεια είναι η ανάπτυξη κατάλληλου κώδικα ο οποίος να επιλέγει την βέλτιστη στρατηγική δυναμικών συναλλαγών.

Αυτό που τελικά έχει πρακτικό νόημα να μελετηθεί στη συνέχεια είναι τα παραπάνω να γίνουν για χαρτοφυλάκια τα οποία περιέχουν πολλές μετοχές μαζί με τα συμβόλαια προαίρεσης αλλά και τεχνικές πρόβλεψης (όπου μπορούμε να λάβουμε υπόψη τυχόν συσχετίσεις τιμών) οι οποίες όμως να μην στηρίζονται μόνο σε παρελθοντικά αριθμητικά δεδομένα αλλά και σε πρόσφατα γεγονότα.

Σημείωση: Διαπιστώστε ότι στο πρόβλημα κατασκευής χαρτοφυλακίου και στο πρόβλημα δυναμικών συναλλαγών απαιτείται μια πρόβλεψη από τον επενδυτή. Αντίθετα, στο πρόβλημα της αποτίμησης δικαιωμάτων προαίρεσης, έτσι όπως το διατυπώσαμε παραπάνω, δεν απαιτείται (και δεν πρέπει) κάποια πρόβλεψη. Αυτό είναι λογικό διότι το πρόβλημα αυτό αφορά δυο επενδυτές (πωλητή και αγοραστή) και αφού οποιαδήποτε πρόβλεψη είναι υποκειμενική ποτέ δεν πρόκειται να συμφωνήσουν τα δυο μέρη. Οι γνωστές μέθοδοι αποτίμησης (Black-Scholes, Binomial κ.τ.λ.) στηρίζονται σε μια πρόβλεψη επομένως δεν υπάρχει κανένας τρόπος βελτίωσης τους και άρα δεν πρόκειται ποτέ να εφαρμοσθούν στην πράξη. Ακόμη χειρότερα, τα γνωστά μοντέλα αποτίμησης δεν δίνουν δίκαιη τιμή στον πραγματικό κόσμο διότι κανείς δεν μπορεί να κατασκευάσει το προτεινόμενο χαρτοφυλάκιο. Αλλά δεν δίνουν ούτε arbitrage free τιμή στον πραγματικό κόσμο διότι, εν γένει, η τιμή θα βρίσκεται έξω από το διάστημα arbitrage free τιμών. Αυτό διότι δεν λαμβάνουν υπόψη τις αξίες των διαθέσιμων συμβολαίων. Η μοναδική τιμή η οποία είναι δίκαιη και arbitrage free εκ κατασκευής είναι η Y^D*.

Αν χρησιμοποιήσετε οποιοδήποτε λογισμικό από τα παραπάνω για πραγματικές επενδύσεις φροντίστε να σχεδιάσετε την προτεινόμενη συνάρτηση κέρδους σε ένα άλλο ανεξάρτητο λογισμικό προκειμένου να σιγουρευτείτε. Αν σας καλύπτει αυτή η συνάρτηση κέρδους τότε μπορείτε να προχωρήσετε στις αντίστοιχες αγοραπωλησίες. Θα πρέπει όμως να προσέξετε ότι αυτές θα πρέπει να γίνουν αρκετά κοντά στις τιμές με τις οποίες έχουν γίνει οι υπολογισμοί.

Στον κώδικα Python Γεωμετρική κίνηση Brown και εφαρμογές μπορείτε να υπολογίσετε τις παραμέτρους μ,σ υποθέτοντας ότι η μετοχή που σας ενδιαφέρει ακολουθεί τη γεωμετρική κίνηση Brown χρησιμοποιώντας παρελθοντικά αριθμητικά δεδομένα από το yahoo finance. Στη συνέχεια μπορείτε να υπολογίσετε την πιθανότητα η αξία της μετοχής να βρεθεί σε κάποιο διάστημα (c,v) αλλά και την πιθανότητα ανόδου. Έχοντας μια τέτοια πρόβλεψη μπορείτε να χρησιμοποιήσετε το λογισμικό για το πως θα κατασκευάσει κάποιος κερδοφόρο χαρτοφυλάκιο στην περίπτωση που η αξία της μετοχής βρεθεί πράγματι στο διάστημα (c,v) (το v μπορεί να είναι και άπειρο). Θα πρέπει όμως να καταλάβετε ότι όποια αποτελέσματα έρχονται από την υπόθεση ότι η αξία της μετοχής ακολουθεί κάποια κατανομή είναι μια πρόβλεψη η οποία στηρίζεται μόνο σε παρελθοντικά αριθμητικά δεδομένα και όχι σε πρόσφατα γεγονότα. Αντίθετα, το λογισμικό κατασκευής χαρτοφυλακίου δεν περιέχει πρόβλεψη αλλά στηρίζεται σε κάποια. Επομένως, το στάδιο της πρόβλεψης είναι σημαντικό αλλά περιέχει ρίσκο ενώ το στάδιο της κατασκευής χαρτοφυλακίου όπως το περιγράψαμε παραπάνω είναι καθαρά ένα μαθηματικό πρόβλημα βελτιστοποίησης.

Στοχαστικές Διαφορικές Εξισώσεις

Για την αριθμητική επίλυση στοχαστικών διαφορικών εξισώσεων των οποίων η ακριβής λύση έχει συγκεκριμένες ιδιότητες, π.χ. θετικότητα (δες για παράδειγμα στοχαστικά μοντέλα για την μοντελοποίηση της αξίας μιας μετοχής) έχουμε προτείνει την λεγόμενη ημι-διακριτή μέθοδο (semi discrete method), δείτε Monte Carlo Methods and Applications καθώς και τις αναφορές εκεί. Για μια σύγκριση με άλλες αριθμητικές μεθόδους μπορεί να δει κανείς την πρόσφατη εργασία Numerical Algorithms η οποία αναφέρεται σε στοχαστικό μοντέλο που εμφανίζεται στην Βιολογία.