Applications & Software
As one can easily observe by studying the above works (as well as corresponding notes), the appropriate buying and selling of options greatly improves the efficiency of a portfolio containing them. In cases where such contracts are not available in the market, portfolio construction leads to the application of Markowitz's theory; therefore, the above theory is a generalization of Markowitz's theory (see problem (9) of the slides Financial Mathematics I).
Often, entire semester courses and even whole books (even recent ones) focus on the valuation (costing) of option contracts rather than their correct application, with the result that students are unable to use them appropriately. Regarding the valuation of these contracts, it should be clear that in practice their prices are determined by the law of supply and demand, as well as the presence of arbitrage opportunities. Therefore, the only thing we can do theoretically is to calculate the price range (by solving problems (10) and (11) of the notes) that does not create an arbitrage opportunity, in order to get an order of magnitude for the value of this contract. Thus, the corresponding valuation theories do not (and never will) lead to a selling price that will ultimately appear in the market, and therefore they have no practical interest. An argument supporting the above conclusion is that because the values of option contracts depend on the underlying stocks, it is impossible to predict their value without first predicting the value of the stocks.
Markowitz's theory does not take into account available option contracts and, therefore, does not transfer risk, forcing one to measure risk (Value at Risk) rather than manage it. However, risk measurement does not lead to static results because the market is dynamic, and thus the corresponding quantity can change drastically the very next day. Risk management, however, is something static and objective, and this is exactly what investors prefer. In full analogy, in Actuarial and Insurance science, risk transfer occurs through the concept of reinsurance. Therefore, a professional should be aware of the available methods of risk transfer and, by solving an optimization problem, arrive at the appropriate strategy for them.
Development of Software with Practical Interest
Our goal is to develop software with practical interest, which we will present here.
-
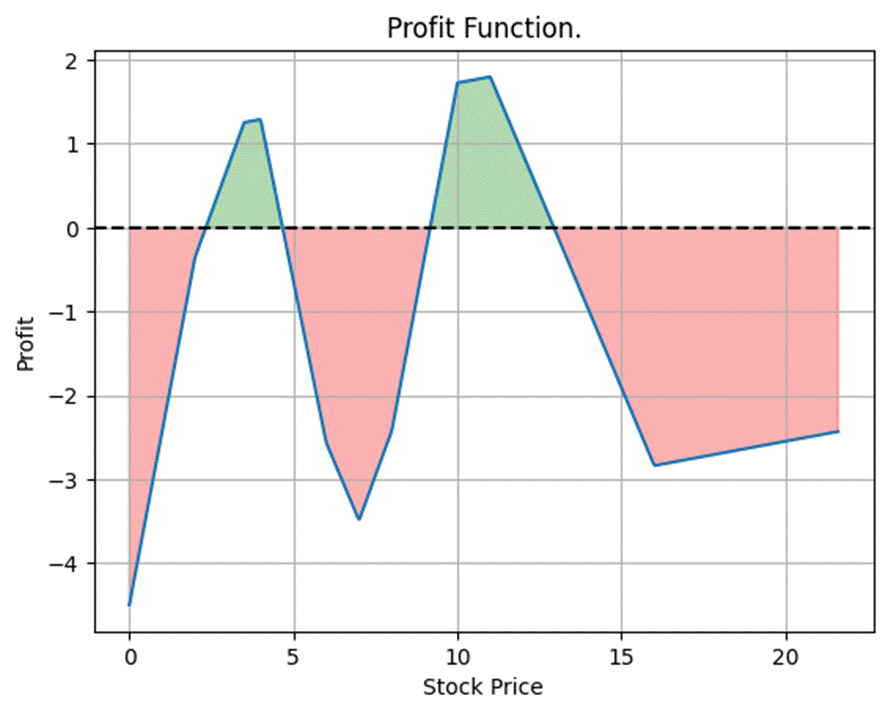
Given a forecast for where the value of a stock will be, by supplying our portfolio with appropriate call and put options, we can construct a portfolio that will profit if the forecast is confirmed, see the figure below. For this purpose, suitable predictive software that also considers recent events would be particularly useful. To achieve this, historical numerical data should be linked to events of the same period, where machine learning, artificial intelligence, etc., will play a significant role. The figure below resulted from using real data (bid-ask spread) with this Python code. In this file, you will also find the corresponding code that identifies, if any, an arbitrage opportunity given a stock and its call and put options.
-
Markowitz's portfolio theory, therefore, has two parts: the first is the investor's forecast, and the second is the construction of the portfolio based on that forecast. In the first part, it uses only past numerical data and is therefore incomplete. In the second part, it does not take into account other assets related to stocks, such as calls and puts. With the methodology we developed, we have greatly improved the second part of portfolio theory, **so with the use of machine learning and artificial intelligence, the first part remains to be improved.**
-
We have built the appropriate Python code with which one can apply Markowitz's theory for as many stocks as desired. It takes real historical numerical data to calculate variances and covariances (Markowitz_Portfolio_Construction.zip).
-
Regarding the option pricing problem, one can use the Python code (FairValueOption) found in the same compressed file. With this code, we can calculate the arbitrage-free interval for the value of a contract with a payoff function f(x) provided by the user, as well as the fair selling price in terms of maximum possible loss. We have proposed other definitions of fair prices, and therefore it is proven that there is no unique such price, while in cases where one exists, it will be that of the definition in terms of maximum possible loss. Note that the payoff function must be piecewise linear with finite branches. In this code, we use real data (bid-ask spread) and it can be applied in practice for pricing any derivative written on a stock, unlike the well-known Black-Scholes, Binomial, etc., pricing models. One can try pricing a simple call option, given that other calls and puts are available in the market, both with the above technique and with the known pricing techniques. By selling/buying a contract at a certain price, the seller/buyer can construct an appropriate hedging portfolio according to their forecasts (see codes WriterHedgingOption1 and BuyerHedgingOption1). We have built the appropriate Python code which calculates the Black-Scholes fair price of any contract written on a stock. It takes real historical numerical data to calculate volatility (Black_Scholes_Fair_Price.zip). Similarly with the binomial model (BinomialModel.zip).
-
Another important topic in financial mathematics is dynamic trading. We have proposed such a process based on the principle "buy low-sell high" and relies more on a forecast concerning the future fluctuation of the stock's value. One such forecasting method is through Stochastic Differential Equations, see below. Our goal subsequently is to develop appropriate code that selects the optimal dynamic trading strategy.
What is ultimately of practical significance to be studied next is to apply the above to portfolios containing multiple stocks along with option contracts, as well as forecasting techniques (where we can account for any price correlations) that are not based solely on past numerical data but also on recent events.
Note: Observe that in the portfolio construction problem and the dynamic trading problem, a forecast from the investor is required. In contrast, in the option pricing problem, as formulated above, no forecast is required (and should not be). This is logical because this problem involves two investors (seller and buyer), and since any forecast is subjective, the two parties will never agree. The well-known pricing methods (Black-Scholes, Binomial, etc.) are based on a forecast; therefore, there is no way to improve them, and thus they will never be applied in practice. Even worse, the known pricing models do not give a fair price in the real world because no one can construct the proposed portfolio. Nor do they provide an arbitrage-free price in the real world because, in general, the price will be outside the arbitrage-free price interval. This is because they do not take into account the values of available contracts. The only price that is fair and arbitrage-free by construction is YD*.
If you use any of the above software for real investments, make sure to plot the proposed profit function in another independent software to ensure accuracy. If this profit function covers your needs, then you can proceed with the corresponding trades. However, you should note that these should be executed reasonably close to the prices used for the calculations.
-
In the Python code Geometric Brownian motion and applications, you can calculate the parameters μ,σ by assuming that the stock you are interested in follows geometric Brownian motion using historical numerical data from Yahoo Finance. You can then calculate the probability that the stock's value will be in a certain interval (c,v) as well as the probability of an increase. Having such a forecast, you can use the software on how to construct a profitable portfolio if the stock's value indeed falls within the interval (c,v) (v can also be infinity). However, you should understand that any results derived from the assumption that the stock's value follows a certain distribution are a forecast based only on past numerical data and not on recent events. In contrast, the portfolio construction software does not contain a forecast but relies on one. Therefore, the forecasting stage is important but involves risk, while the portfolio construction stage, as described above, is purely a mathematical optimization problem.
Stochastic Differential Equations
For the numerical solution of stochastic differential equations whose exact solution has specific properties, e.g., positivity (see, for example, stochastic models for modeling the value of a stock), we have proposed the so-called semi-discrete method, see Monte Carlo Methods and Applications as well as the references therein. For a comparison with other numerical methods, one can refer to the recent work Numerical Algorithms which refers to a stochastic model appearing in Biology.